Triangle Midsegment Theorem Worksheet Fun

Unlocking the Secrets of Triangle Midsegment Theorem

Are you ready to explore the fascinating world of triangles and midsegments? In this fun and interactive worksheet, we’ll delve into the Triangle Midsegment Theorem, a fundamental concept in geometry that will help you better understand the properties of triangles.

What is the Triangle Midsegment Theorem?

The Triangle Midsegment Theorem states that the segment joining the midpoints of two sides of a triangle is parallel to the third side and is half as long as the third side. Mathematically, this can be expressed as:

Theorem: In a triangle ABC, if D and E are the midpoints of AB and AC, respectively, then DE is parallel to BC and DE = ¹⁄₂ BC.

Proving the Theorem

To prove the Triangle Midsegment Theorem, we can use a variety of methods, including coordinate geometry, vectors, or even pure geometric reasoning. Here’s a step-by-step proof using coordinate geometry:

1. Let’s assume the coordinates of A, B, and C are (x1, y1), (x2, y2), and (x3, y3), respectively.
2. Since D and E are the midpoints of AB and AC, their coordinates are ((x1+x2)/2, (y1+y2)/2) and ((x1+x3)/2, (y1+y3)/2), respectively.
3. Using the midpoint formula, we can find the coordinates of the point F, which is the midpoint of BC. The coordinates of F are ((x2+x3)/2, (y2+y3)/2).
4. Now, let’s find the slope of DE and BC. The slope of DE is (y2-y1)/(x2-x1), and the slope of BC is (y3-y2)/(x3-x2).
5. By equating the slopes of DE and BC, we can show that DE is parallel to BC.
6. Finally, we can use the distance formula to show that DE = ¹⁄₂ BC.

🤔 Note: The proof involves some intricate calculations, but the key idea is to use the midpoint formula and the slope formula to establish the relationship between DE and BC.

Practice Problems

Now that we’ve explored the Triangle Midsegment Theorem, it’s time to put your knowledge to the test! Try solving these practice problems:

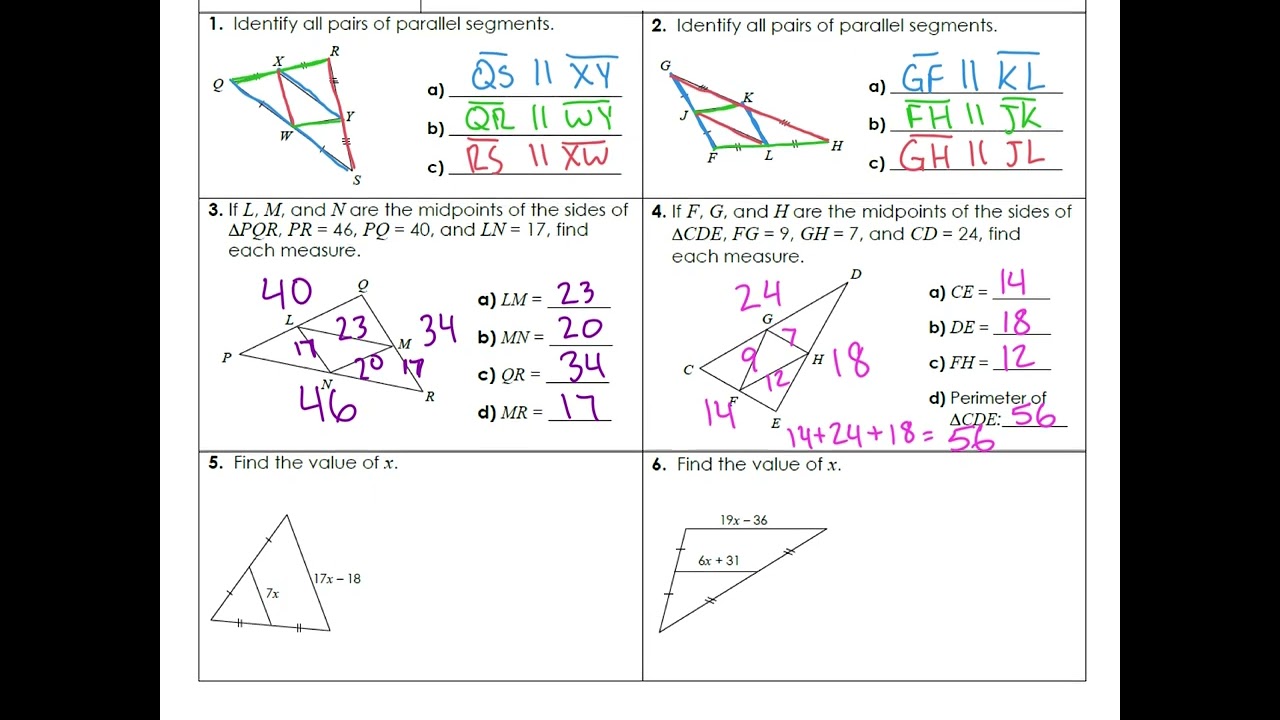
Problem 1: In triangle ABC, D and E are the midpoints of AB and AC, respectively. If BC = 10 cm, find the length of DE.

Problem 2: In triangle XYZ, M and N are the midpoints of XY and XZ, respectively. If MN = 6 cm, find the length of YZ.

Problem 3: In triangle PQR, S and T are the midpoints of PQ and PR, respectively. If ST = 8 cm, find the length of QR.

Solutions

Solution 1: Using the Triangle Midsegment Theorem, we know that DE = ¹⁄₂ BC. Since BC = 10 cm, DE = ¹⁄₂ × 10 = 5 cm.

Solution 2: Using the Triangle Midsegment Theorem, we know that MN = ¹⁄₂ YZ. Since MN = 6 cm, YZ = 2 × 6 = 12 cm.

Solution 3: Using the Triangle Midsegment Theorem, we know that ST = ¹⁄₂ QR. Since ST = 8 cm, QR = 2 × 8 = 16 cm.

Real-World Applications

The Triangle Midsegment Theorem has numerous real-world applications, from architecture to engineering. Here are a few examples:

• Architecture: The theorem can be used to design buildings and bridges, ensuring that they are structurally sound and aesthetically pleasing.
• Engineering: The theorem can be used to optimize the design of mechanical systems, such as gears and linkages.
• Computer Science: The theorem can be used in computer graphics and game development to create realistic simulations and models.

Conclusion

In conclusion, the Triangle Midsegment Theorem is a fundamental concept in geometry that has numerous real-world applications. By understanding this theorem, you can develop a deeper appreciation for the beauty and complexity of triangles. So, keep exploring and practicing, and soon you’ll become a master of triangle midsegments!

Related Terms:

• Triangle midsegment worksheet pdf
• Triangle Inequality Theorem Worksheet
• Triangle Proportionality Theorem worksheet