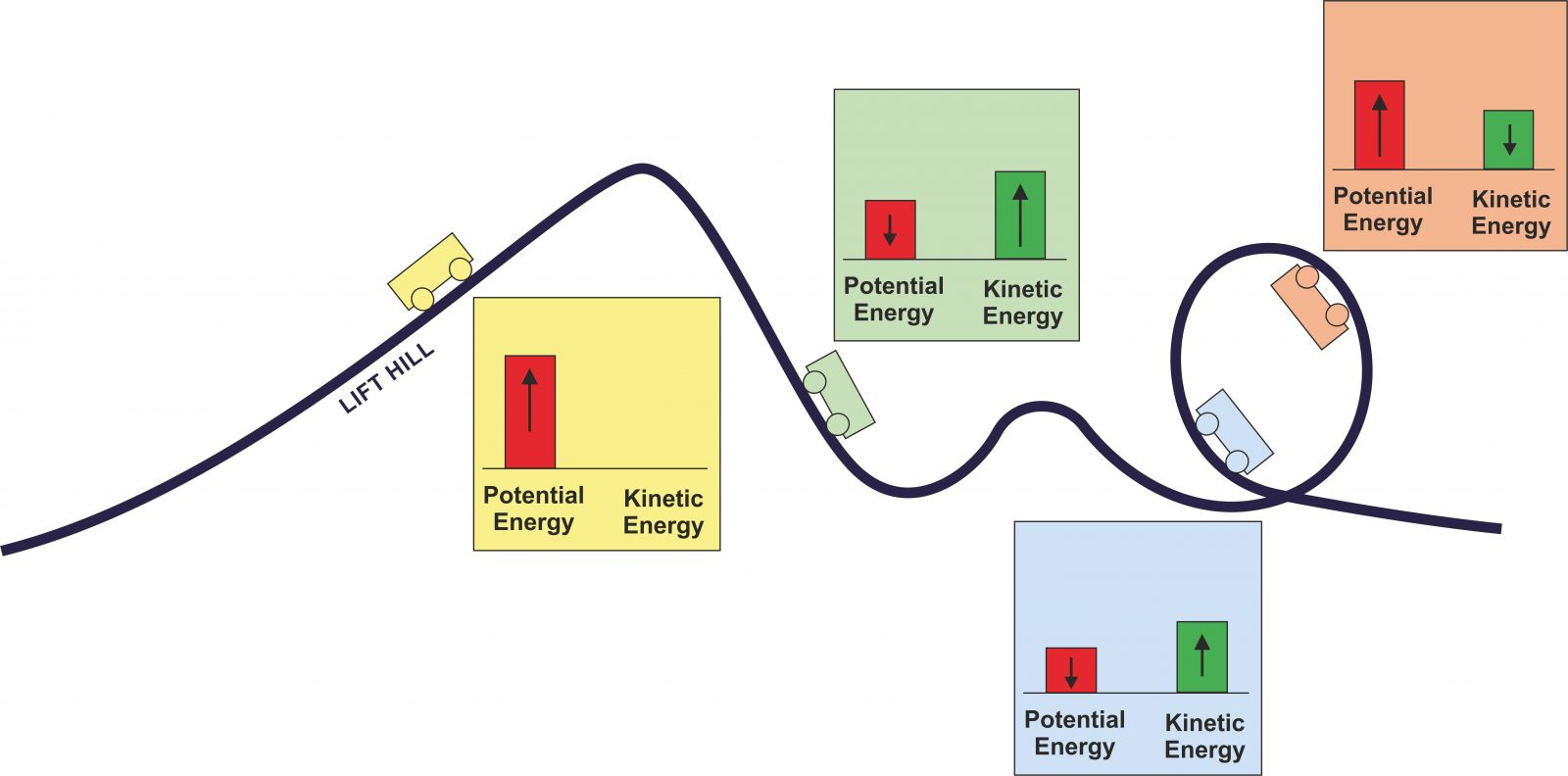
Graphing Linear Inequalities Worksheet for Easy Math Solutions

Graphing Linear Inequalities: A Step-by-Step Guide
Linear inequalities are a fundamental concept in mathematics, and graphing them is an essential skill for problem-solving. In this post, we will delve into the world of linear inequalities, exploring what they are, how to graph them, and providing a comprehensive worksheet for practice.
What are Linear Inequalities?
Linear inequalities are mathematical statements that compare two expressions using inequality symbols (<, >, ≤, ≥). They are used to represent relationships between variables and constants. For example:
2x + 3 > 5
This linear inequality states that the sum of 2 times x and 3 is greater than 5.
How to Graph Linear Inequalities
Graphing linear inequalities involves drawing a line on a coordinate plane and shading the region that satisfies the inequality. Here’s a step-by-step guide:
- Write the inequality in slope-intercept form: Convert the linear inequality to slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept.
- Graph the boundary line: Draw the line on the coordinate plane using the slope and y-intercept. Use a solid line for ≤ and ≥ inequalities and a dashed line for < and > inequalities.
- Shade the region: Determine which region of the plane satisfies the inequality. Use a test point to check which side of the line satisfies the inequality. Shade the region accordingly.
📝 Note: The boundary line is included in the solution set for ≤ and ≥ inequalities but not for < and > inequalities.
Graphing Linear Inequalities Examples
Example 1: x + 2y ≤ 4
- Write the inequality in slope-intercept form: y ≤ -1/2x + 2
- Graph the boundary line: Draw a solid line with a slope of -1⁄2 and a y-intercept of 2.
- Shade the region: Test a point (e.g., (0, 0)) to determine which region satisfies the inequality. Shade the region below the line.
Example 2: 3x - 2y > 6
- Write the inequality in slope-intercept form: y < 3/2x - 3
- Graph the boundary line: Draw a dashed line with a slope of 3⁄2 and a y-intercept of -3.
- Shade the region: Test a point (e.g., (0, 0)) to determine which region satisfies the inequality. Shade the region above the line.
Graphing Linear Inequalities Worksheet
Here’s a comprehensive worksheet to practice graphing linear inequalities:

| Inequality | Slope-Intercept Form | Boundary Line | Shaded Region |
|---|---|---|---|
| x + 3y ≤ 6 | y ≤ -1/3x + 2 | Solid line with slope -1⁄3 and y-intercept 2 | Below the line |
| 2x - 4y > 8 | y < 1/2x - 2 | Dashed line with slope 1⁄2 and y-intercept -2 | Above the line |
| x + 2y ≥ 4 | y ≥ -1/2x + 2 | Solid line with slope -1⁄2 and y-intercept 2 | On or above the line |
| 3x - 2y ≤ 6 | y ≥ 3/2x - 3 | Solid line with slope 3⁄2 and y-intercept -3 | On or below the line |
Additional Practice Exercises
- Graph the linear inequality: x + 2y > 3
- Graph the linear inequality: 2x - 3y ≤ 6
- Graph the linear inequality: y < 2x + 1
Conclusion
Graphing linear inequalities is a fundamental skill in mathematics that requires attention to detail and practice. By following the step-by-step guide and practicing with the provided worksheet, you’ll become proficient in graphing linear inequalities and develop a solid understanding of this essential concept.
What is the difference between ≤ and < in linear inequalities?
+The main difference is that ≤ includes the boundary line, while < does not. When graphing, use a solid line for ≤ and a dashed line for <.
Can I use a calculator to graph linear inequalities?
+Yes, you can use a graphing calculator to graph linear inequalities. However, it’s essential to understand the underlying concepts and be able to graph them manually as well.
How do I determine which region to shade when graphing a linear inequality?
+Choose a test point (e.g., (0, 0)) and plug it into the inequality. If the statement is true, shade the region containing the test point. If the statement is false, shade the other region.