Mixed Fraction Worksheet for Easy Math Practice

Mixed Fractions: A Comprehensive Guide to Easy Math Practice
Are you or your students struggling with mixed fractions? Do you find it challenging to simplify or compare them? Worry no more! This guide is designed to provide a thorough understanding of mixed fractions, along with a worksheet to help you practice and reinforce your knowledge.
What are Mixed Fractions?
A mixed fraction is a combination of a whole number and a proper fraction. It represents a value that is greater than a whole number but not a whole number itself. For example, 2 3⁄4 is a mixed fraction that represents two whole units and three-quarters of another unit.
Why are Mixed Fractions Important?
Mixed fractions are essential in various real-life situations, such as:
- Measuring ingredients for cooking or baking
- Calculating distances or speeds
- Understanding time and schedules
- Solving problems in physics and engineering
How to Simplify Mixed Fractions
Simplifying mixed fractions involves converting them to improper fractions or reducing them to their lowest terms. Here’s a step-by-step guide:
- Convert to an improper fraction: Multiply the whole number by the denominator, then add the numerator. Write the result as an improper fraction.
- Reduce to lowest terms: Divide both the numerator and denominator by their greatest common divisor (GCD).
Example: Simplify the mixed fraction 3 2⁄4.
- Convert to an improper fraction: 3 × 4 + 2 = 14⁄4
- Reduce to lowest terms: 14 ÷ 2 = 7, 4 ÷ 2 = 2
- Simplified answer: 7⁄2
Mixed Fraction Worksheet
Practice your mixed fraction skills with this worksheet:
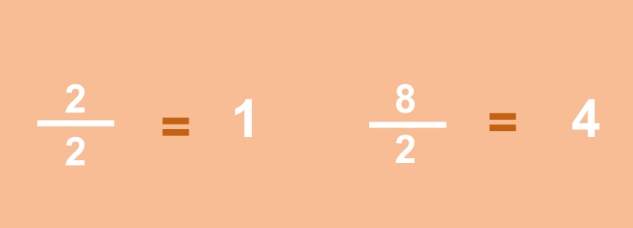
| Problem | Answer |
|---|---|
| 1. Simplify: 2 3⁄4 | |
| 2. Compare: 3 1⁄2 and 2 3⁄4 | |
| 3. Add: 2 1⁄4 + 1 3⁄4 | |
| 4. Subtract: 4 2⁄3 - 2 1⁄3 | |
| 5. Multiply: 2 1⁄2 × 3 3⁄4 | |
| 6. Divide: 6 3⁄4 ÷ 2 1⁄2 | |
| 7. Simplify: 5 3⁄8 | |
| 8. Compare: 2 3⁄4 and 3 1⁄2 | |
| 9. Add: 3 1⁄2 + 2 1⁄4 | |
| 10. Subtract: 5 2⁄3 - 3 1⁄3 |
Answers:
- 11⁄4
- 3 1⁄2 is greater
- 4
- 2 1⁄6
- 9 1⁄2
- 3 1⁄4
- 43⁄8
- 2 3⁄4 is less
- 5 3⁄4
- 2 1⁄6
📝 Note: Make sure to show your work and explain your answers to get the most out of this worksheet.
Tips and Tricks
- When adding or subtracting mixed fractions, make sure to align the whole numbers and fractions separately.
- When multiplying or dividing mixed fractions, convert them to improper fractions first.
- To compare mixed fractions, convert them to equivalent decimals or fractions.
Common Mistakes to Avoid
- Forgetting to convert mixed fractions to improper fractions when simplifying or comparing.
- Not reducing fractions to their lowest terms.
- Making calculation errors when adding, subtracting, multiplying, or dividing mixed fractions.
Conclusion
Mixed fractions can be challenging, but with practice and patience, you can master them. Remember to simplify, compare, and perform operations with confidence. Use the worksheet and tips provided to reinforce your understanding and become a math whiz!
What is the difference between a mixed fraction and an improper fraction?
+A mixed fraction is a combination of a whole number and a proper fraction, while an improper fraction is a fraction that has a numerator greater than its denominator.
How do I convert a mixed fraction to an improper fraction?
+Multiply the whole number by the denominator, then add the numerator. Write the result as an improper fraction.
Why is it important to reduce fractions to their lowest terms?
+Reducing fractions to their lowest terms makes them easier to compare and perform operations with. It also helps to avoid calculation errors.
Related Terms:
- Multiplying Fractions worksheet pdf
- Subtracting fractions Worksheet
- Fraction Worksheet Grade 5
- Fraction to decimal Grade 4



