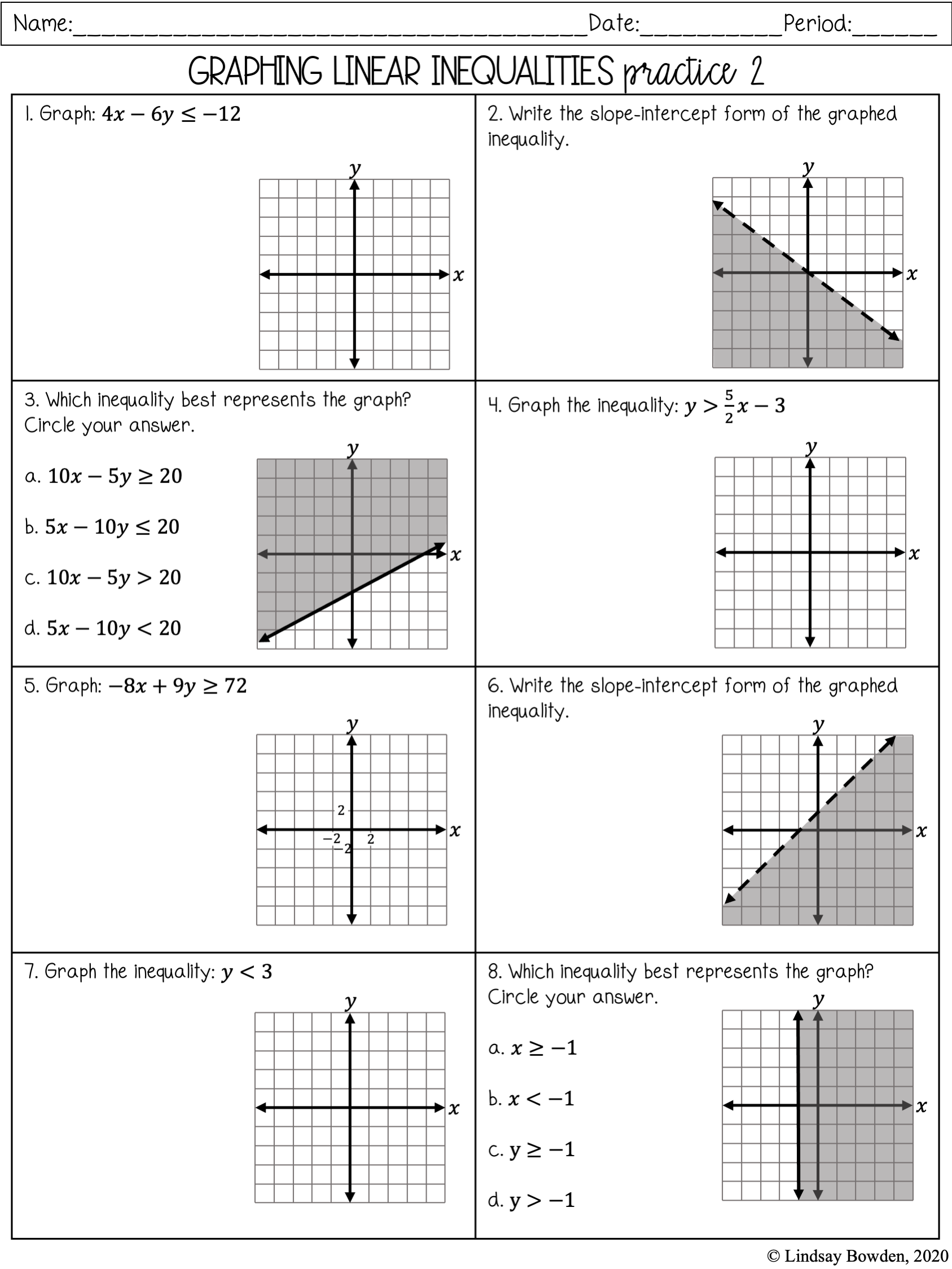
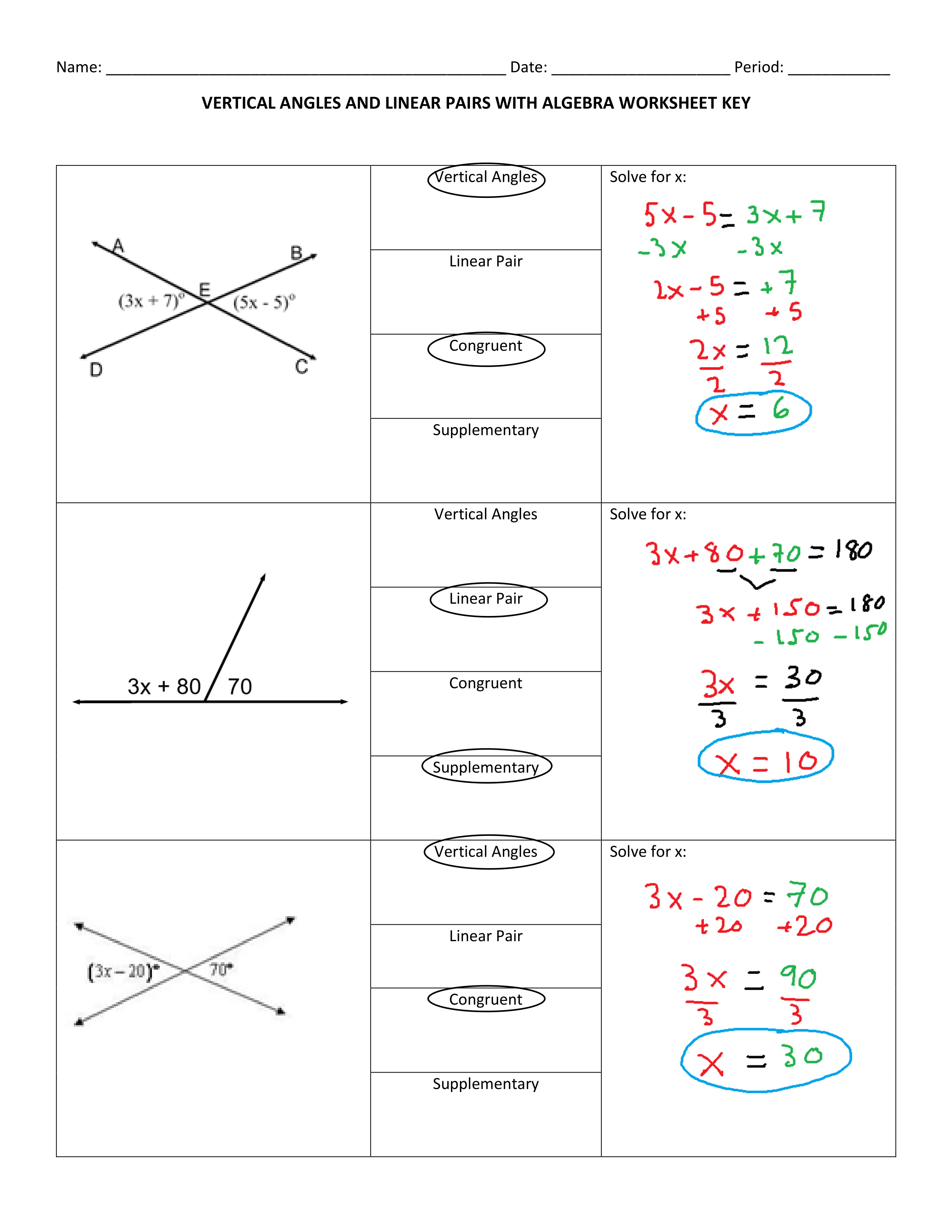
5 Ways to Graph Quadratics from Standard Form
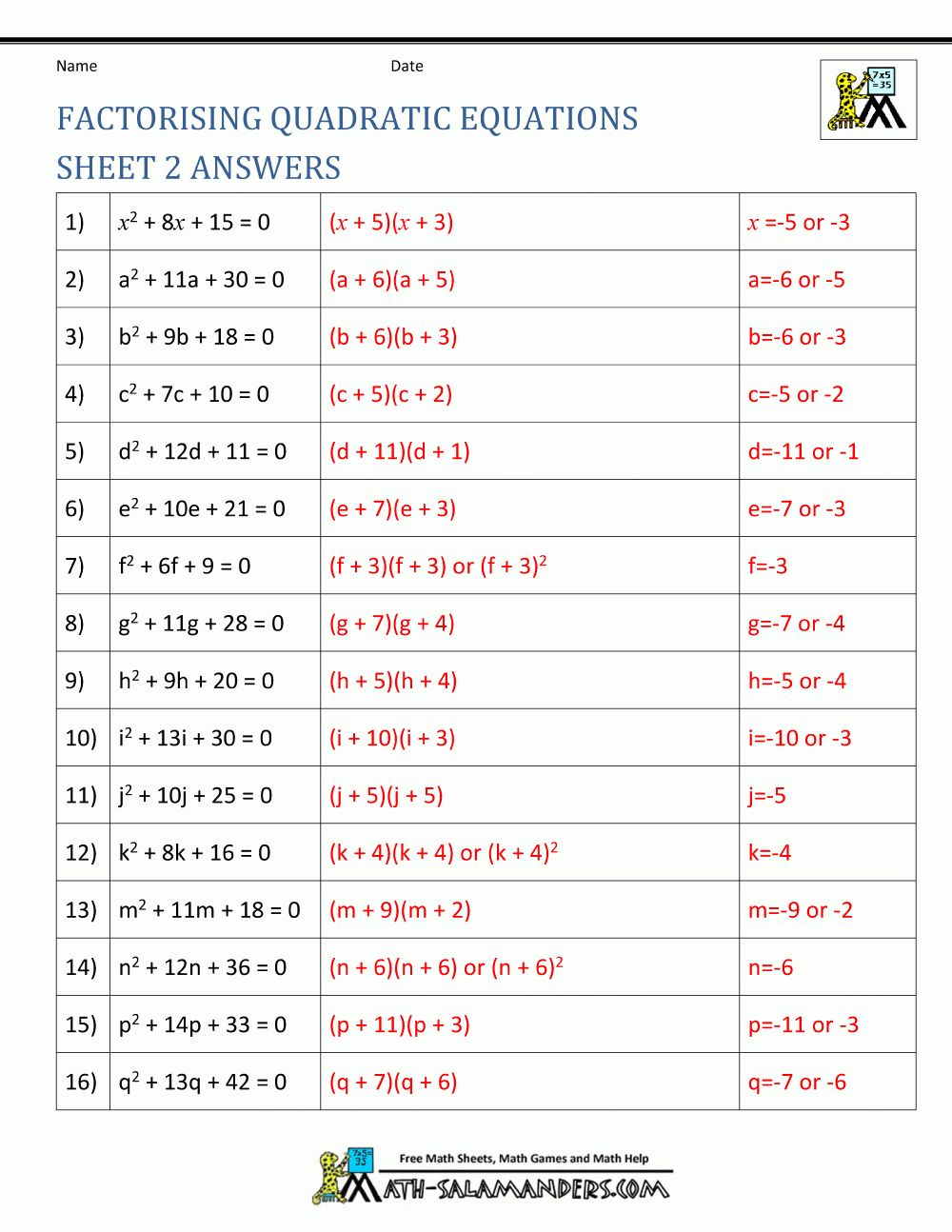
Unlocking the Secrets of Quadratic Graphs: A Comprehensive Guide
Quadratic equations are a fundamental concept in algebra, and graphing them is an essential skill for any student or math enthusiast. While graphing quadratics can seem intimidating at first, breaking down the process into manageable steps can make it more accessible. In this article, we will explore five ways to graph quadratics from standard form, using a combination of algebraic manipulation and visual aids.
Method 1: Factoring
Factoring is a popular method for graphing quadratics, as it allows us to easily identify the roots (or x-intercepts) of the equation. To factor a quadratic in standard form, we need to find two numbers whose product is the constant term © and whose sum is the coefficient of the linear term (b).
Example: Graph the quadratic equation x^2 + 5x + 6 = 0 by factoring.
- Factor the quadratic: (x + 3)(x + 2) = 0
- Identify the roots: x + 3 = 0 or x + 2 = 0
- Solve for x: x = -3 or x = -2
- Graph the roots on the x-axis
Using this method, we can quickly identify the roots of the equation and graph them on the x-axis. However, factoring may not always be possible, especially for more complex quadratics.
Method 2: Completing the Square
Completing the square is a powerful technique for graphing quadratics, as it allows us to rewrite the equation in vertex form. To complete the square, we need to add and subtract a constant term to create a perfect square trinomial.
Example: Graph the quadratic equation x^2 + 6x + 8 = 0 by completing the square.
- Add and subtract a constant term: x^2 + 6x + 9 - 1 = 0
- Rewrite as a perfect square trinomial: (x + 3)^2 - 1 = 0
- Identify the vertex: (h, k) = (-3, -1)
- Graph the vertex and the parabola
By completing the square, we can rewrite the quadratic equation in vertex form and easily identify the vertex of the parabola.
Method 3: Using the Quadratic Formula
The quadratic formula is a versatile tool for graphing quadratics, as it allows us to find the roots of the equation even when factoring or completing the square is not possible. To use the quadratic formula, we need to plug in the values of a, b, and c into the formula:
x = (-b ± √(b^2 - 4ac)) / 2a
Example: Graph the quadratic equation x^2 + 4x + 5 = 0 using the quadratic formula.
- Plug in the values: x = (-(4) ± √((4)^2 - 4(1)(5))) / 2(1)
- Simplify the expression: x = (-4 ± √(16 - 20)) / 2
- Solve for x: x = (-4 ± √(-4)) / 2
- Graph the complex roots
Using the quadratic formula, we can find the roots of the equation even when they are complex. However, this method may not provide as much visual insight as other methods.
Method 4: Graphing with a Table of Values
Graphing with a table of values is a straightforward method that involves creating a table of x-values and corresponding y-values. This method is useful when we want to visualize the graph of the quadratic equation without relying on algebraic manipulations.
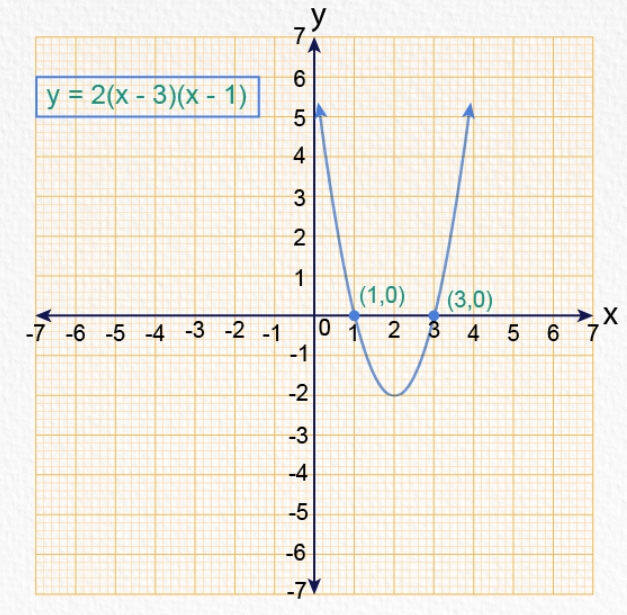
Example: Graph the quadratic equation x^2 + 2x + 1 = 0 using a table of values.
| x | y |
|---|---|
| -3 | 16 |
| -2 | 9 |
| -1 | 4 |
| 0 | 1 |
| 1 | 4 |
| 2 | 9 |
| 3 | 16 |
By creating a table of values, we can visualize the graph of the quadratic equation and identify key features such as the vertex and axis of symmetry.
Method 5: Using Graphing Software
Graphing software is a powerful tool that allows us to visualize the graph of a quadratic equation quickly and accurately. By entering the equation into the software, we can generate a graph and explore its properties.
Example: Graph the quadratic equation x^2 + 3x + 2 = 0 using graphing software.
Using graphing software, we can create an accurate graph of the quadratic equation and explore its properties, such as the vertex, axis of symmetry, and x-intercepts.
📝 Note: When using graphing software, make sure to check the equation for accuracy and adjust the window settings as needed to visualize the entire graph.
In conclusion, graphing quadratics from standard form requires a combination of algebraic manipulation and visual aids. By mastering these five methods, we can unlock the secrets of quadratic graphs and develop a deeper understanding of this fundamental concept in algebra.
What is the standard form of a quadratic equation?
+The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants.
How do I determine the vertex of a quadratic equation?
+The vertex of a quadratic equation can be determined by completing the square or using the formula (h, k) = (-b / 2a, f(-b / 2a)).
Can I graph a quadratic equation with a table of values?
+Yes, you can graph a quadratic equation with a table of values by creating a table of x-values and corresponding y-values.
Related Terms:
- Graphing Quadratics Worksheet pdf
- Graphing Quadratics Worksheet with answers