Vertical Angles and Linear Pairs Practice Made Easy

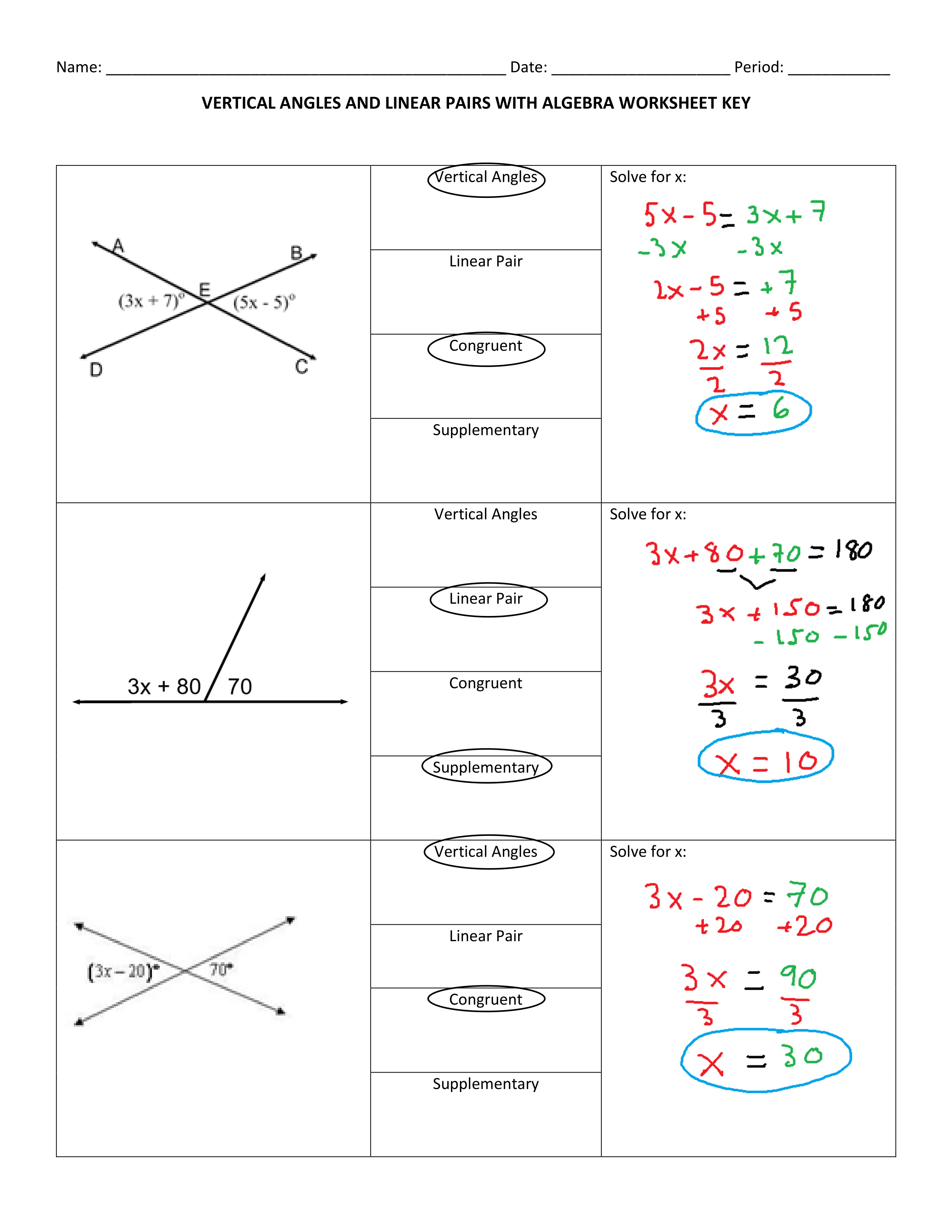
Unlocking the Secrets of Vertical Angles and Linear Pairs

When it comes to geometry, understanding vertical angles and linear pairs is crucial for solving various problems. These concepts may seem complex at first, but with practice and the right approach, you can master them easily. In this post, we will delve into the world of vertical angles and linear pairs, exploring their definitions, properties, and providing practice exercises to help you reinforce your understanding.

What are Vertical Angles?

Vertical angles are a pair of angles that are opposite each other when two lines intersect. They are called “vertical” because they share the same vertex (corner point) and are formed by the intersection of two lines.

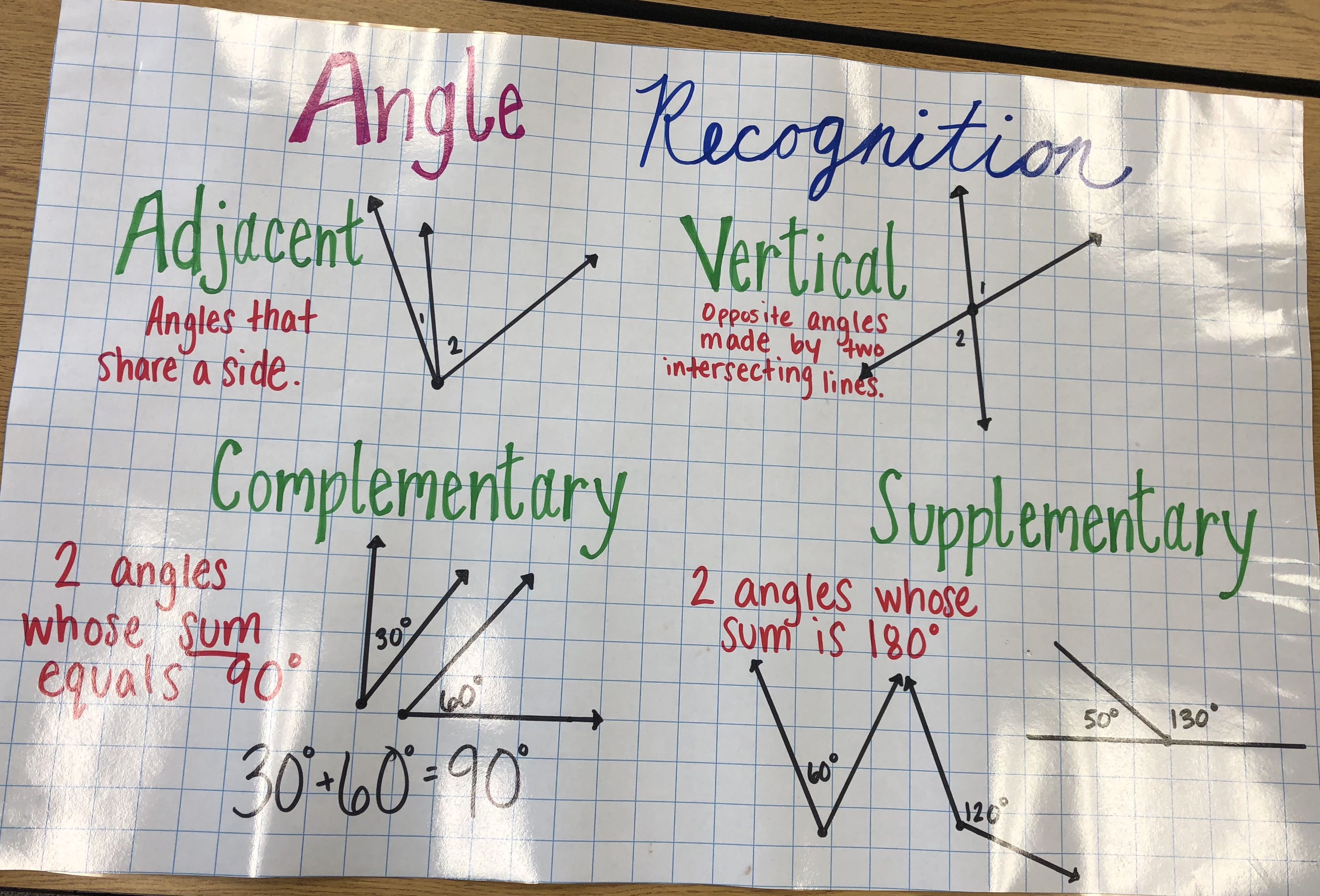
Definition:	Example:
Vertical angles are a pair of angles that are opposite each other when two lines intersect.

As you can see from the diagram, the two angles labeled ∠AED and ∠AEB are vertical angles because they share the same vertex (point A) and are formed by the intersection of two lines.

What are Linear Pairs?

A linear pair is a pair of adjacent angles that form a straight line. In other words, they are two angles that are next to each other and together form a straight angle (180°).

Definition:	Example:
A linear pair is a pair of adjacent angles that form a straight line.

As you can see from the diagram, the two angles labeled ∠AEC and ∠AED are a linear pair because they are adjacent to each other and together form a straight angle (180°).

Properties of Vertical Angles and Linear Pairs

Now that we have defined vertical angles and linear pairs, let’s explore some of their properties:

• Vertical Angles are Congruent: Vertical angles are always equal in measure. This means that if you have two vertical angles, you can be sure that they are congruent.
• Linear Pairs are Supplementary: Linear pairs are always supplementary, meaning that their measures add up to 180°.

🔍 Note: When working with vertical angles and linear pairs, it's essential to keep in mind that the properties mentioned above are always true, unless otherwise stated in the problem.

Practice Exercises

Now it’s time to put your understanding of vertical angles and linear pairs to the test! Try solving the following practice exercises:

• If ∠AED and ∠AEB are vertical angles and m∠AED = 60°, what is the measure of ∠AEB?
• If ∠AEC and ∠AED are a linear pair and m∠AEC = 70°, what is the measure of ∠AED?
• If two lines intersect, forming vertical angles ∠AED and ∠AEB, and m∠AED = 2x, what is the measure of ∠AEB in terms of x?

Take your time, and don’t be afraid to ask for help if you need it. Remember to apply the properties of vertical angles and linear pairs to solve these exercises.

Tips and Tricks

Here are some tips and tricks to keep in mind when working with vertical angles and linear pairs:

• Always identify the vertical angles and linear pairs in a diagram before starting to solve the problem.
• Use the properties of vertical angles and linear pairs to simplify the problem and make it easier to solve.
• Pay attention to the measures of the angles and use algebraic expressions to solve for unknown angles.

By following these tips and practicing regularly, you’ll become a pro at working with vertical angles and linear pairs in no time!

Conclusion

Vertical angles and linear pairs are essential concepts in geometry that can seem daunting at first, but with practice and the right approach, you can master them easily. Remember to apply the properties of vertical angles and linear pairs to solve problems, and don’t be afraid to ask for help if you need it. With time and practice, you’ll become confident in your ability to work with these concepts and tackle even the toughest geometry problems.

Related Terms:

• Adjacent angles Worksheet pdf
• Linear pair Worksheet pdf
• Vertical angles Worksheet Kuta