Solving Inequalities Made Easy Practice Worksheet
Introduction to Solving Inequalities
Inequalities are mathematical statements that compare two expressions, stating that one is greater than, less than, or equal to the other. Solving inequalities is a crucial skill in mathematics, and with practice, you can master it. In this post, we will guide you through the steps to solve inequalities and provide a practice worksheet to help you improve your skills.
What are Inequalities?
Inequalities are mathematical statements that contain the following symbols:
- Greater than (>)
- Less than (<)
- Greater than or equal to (≥)
- Less than or equal to (≤)
For example:
- 2x + 3 > 5
- x - 2 < 3
- x ≥ 4
- x ≤ 2
Types of Inequalities
There are two main types of inequalities:
- Linear inequalities: These are inequalities that contain only linear expressions, such as 2x + 3 > 5.
- Non-linear inequalities: These are inequalities that contain non-linear expressions, such as x^2 + 3 > 5.
Steps to Solve Inequalities
To solve inequalities, follow these steps:
- Add or subtract the same value to both sides: This will help you isolate the variable.
- Multiply or divide both sides by the same value: Be careful when multiplying or dividing by a negative number, as this will change the direction of the inequality.
- Simplify the inequality: Combine like terms and simplify the expression.
📝 Note: When multiplying or dividing both sides by a negative number, flip the inequality sign.
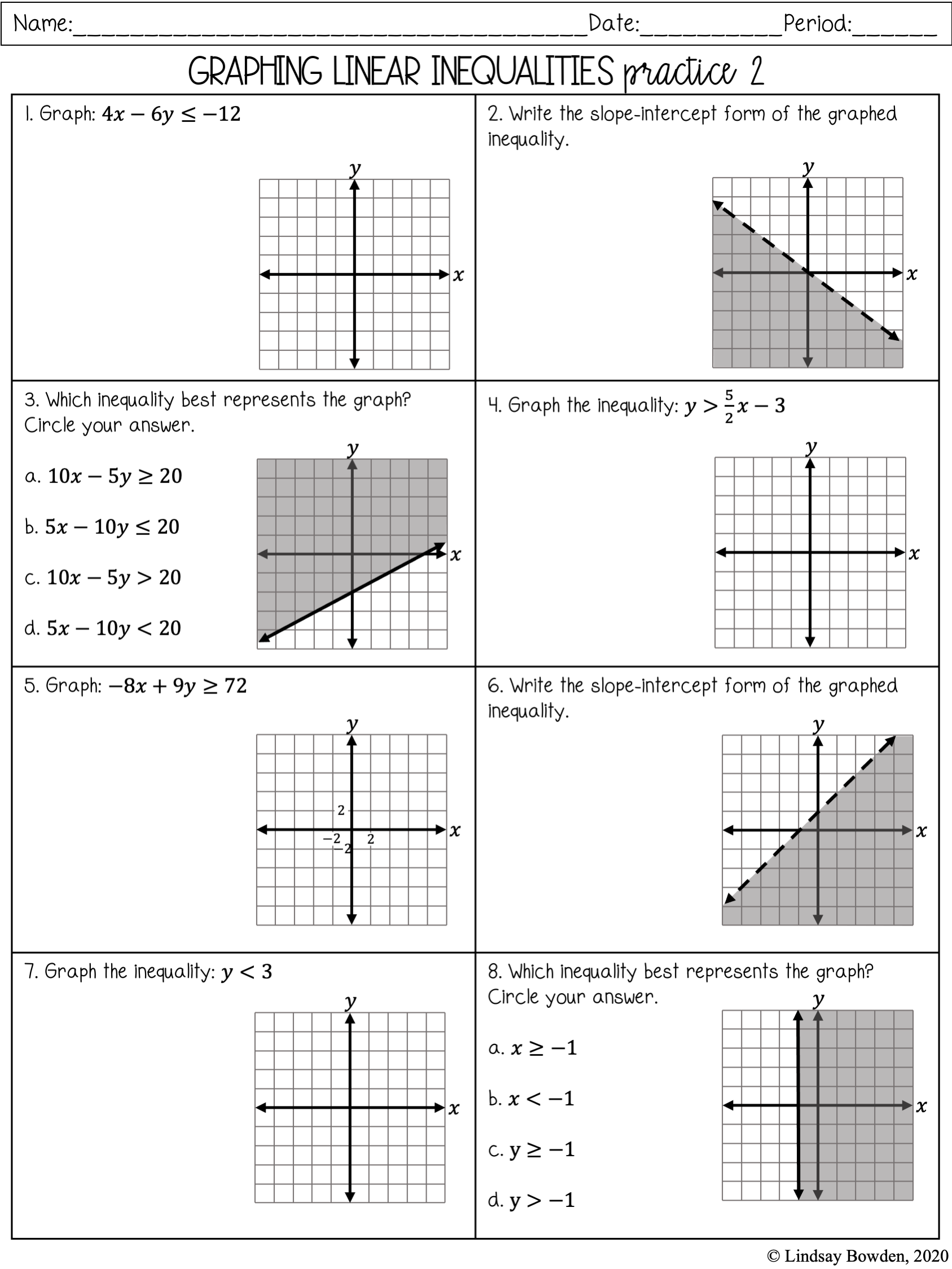
Practice Worksheet
Here are some inequality problems for you to practice:
Section 1: Linear Inequalities

| Inequality | Solution |
|---|---|
| 2x + 3 > 5 | |
| x - 2 < 3 | |
| x ≥ 4 | |
| x ≤ 2 |
Section 2: Non-Linear Inequalities
| Inequality | Solution |
|---|---|
| x^2 + 3 > 5 | |
| x^2 - 2 < 3 | |
| x^2 ≥ 4 | |
| x^2 ≤ 2 |
Solutions
Section 1: Linear Inequalities
| Inequality | Solution |
|---|---|
| 2x + 3 > 5 | x > 1 |
| x - 2 < 3 | x < 5 |
| x ≥ 4 | x ≥ 4 |
| x ≤ 2 | x ≤ 2 |
Section 2: Non-Linear Inequalities
| Inequality | Solution |
|---|---|
| x^2 + 3 > 5 | x > 1 or x < -1 |
| x^2 - 2 < 3 | -1 < x < 1 |
| x^2 ≥ 4 | x ≥ 2 or x ≤ -2 |
| x^2 ≤ 2 | -√2 ≤ x ≤ √2 |
Tips and Tricks
- Always check your solutions by plugging them back into the original inequality.
- Use a number line to visualize the solution set.
- Practice, practice, practice! The more you practice, the more comfortable you will become with solving inequalities.
What is the difference between an equation and an inequality?
+An equation states that two expressions are equal, while an inequality states that one expression is greater than, less than, or equal to another.
How do I know when to flip the inequality sign?
+Flip the inequality sign when multiplying or dividing both sides by a negative number.
Can I use a calculator to solve inequalities?
+While calculators can be helpful, it's essential to understand the steps to solve inequalities manually, as calculators may not always provide the correct solution.
Now that you’ve practiced solving inequalities, you should feel more confident in your ability to tackle these types of problems. Remember to always check your solutions and use a number line to visualize the solution set. With practice and patience, you’ll become a pro at solving inequalities!
Related Terms:
- Linear Inequalities worksheet
- Inequalities problems and solutions
- Inequality Word Problems Worksheet
- Equation and inequality worksheet
- Linear graph Worksheet pdf
- Worksheet math grade 6