5 Ways to Master the Distance Formula Worksheet
Mastering the Distance Formula Worksheet: A Comprehensive Guide
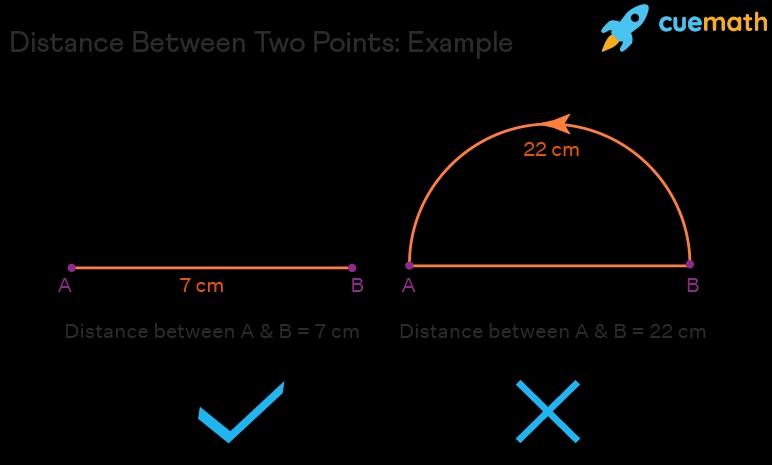
The distance formula is a fundamental concept in mathematics, used to calculate the distance between two points in a coordinate plane. However, for many students, working with distance formula worksheets can be a daunting task. In this article, we will explore five ways to master the distance formula worksheet, providing you with a comprehensive guide to overcome any challenges you may face.
Understanding the Distance Formula
Before we dive into the strategies for mastering the distance formula worksheet, it’s essential to understand the formula itself. The distance formula is derived from the Pythagorean theorem and is used to calculate the distance between two points (x1, y1) and (x2, y2) in a coordinate plane. The formula is:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Where d is the distance between the two points.
1. Visualize the Coordinate Plane
To master the distance formula worksheet, it’s crucial to visualize the coordinate plane. Imagine the x-axis and y-axis intersecting to form a grid. Each point on the grid has a unique set of coordinates (x, y). Visualizing the coordinate plane will help you understand how to apply the distance formula to calculate the distance between two points.
🔍 Note: Take a moment to review the coordinate plane and familiarize yourself with the x-axis and y-axis.
2. Break Down the Formula
Breaking down the distance formula into smaller components will help you understand how to apply it. The formula consists of three main parts:
- The difference between the x-coordinates (x2 - x1)
- The difference between the y-coordinates (y2 - y1)
- The square root of the sum of the squared differences
By breaking down the formula, you’ll be able to identify the individual components and calculate the distance between two points more efficiently.
3. Practice with Sample Problems
Practice is key to mastering the distance formula worksheet. Start with simple sample problems, such as calculating the distance between two points on the x-axis or y-axis. Gradually move on to more complex problems, such as calculating the distance between two points in the coordinate plane.
Here’s a sample problem:
Find the distance between the points (3, 4) and (6, 8).
Using the distance formula:
d = √((6 - 3)^2 + (8 - 4)^2) d = √(3^2 + 4^2) d = √(9 + 16) d = √25 d = 5
4. Use Real-World Applications
To make the distance formula more engaging and relevant, use real-world applications. For example, you can use the distance formula to calculate the distance between two cities on a map or the distance between two objects in a room.
Here’s a real-world example:
A pilot is flying from City A (30° N, 40° W) to City B (50° N, 60° W). What is the distance between the two cities?
Using the distance formula:
d = √((50 - 30)^2 + (60 - 40)^2) d = √(20^2 + 20^2) d = √(400 + 400) d = √800 d = 28.28 miles
5. Create a Worksheet Template
To streamline your practice sessions, create a worksheet template with the distance formula and space to plug in values. This will help you stay organized and focused as you work through sample problems.

| Point 1 (x1, y1) | Point 2 (x2, y2) | Distance (d) |
|---|---|---|
| (x1, y1) | (x2, y2) | √((x2 - x1)^2 + (y2 - y1)^2) |
By following these five strategies, you’ll be well on your way to mastering the distance formula worksheet. Remember to visualize the coordinate plane, break down the formula, practice with sample problems, use real-world applications, and create a worksheet template.
Now that you’ve mastered the distance formula worksheet, you can confidently tackle more complex math problems and develop a deeper understanding of geometry and trigonometry.
What is the distance formula?
+The distance formula is a mathematical formula used to calculate the distance between two points in a coordinate plane. It is derived from the Pythagorean theorem and is given by the formula: d = √((x2 - x1)^2 + (y2 - y1)^2).
How do I visualize the coordinate plane?
+To visualize the coordinate plane, imagine the x-axis and y-axis intersecting to form a grid. Each point on the grid has a unique set of coordinates (x, y). You can use graph paper or online tools to help you visualize the coordinate plane.
What are some real-world applications of the distance formula?
+The distance formula has many real-world applications, including calculating the distance between two cities, the distance between two objects in a room, and the distance between two points on a map.
Related Terms:
- Distance formula Worksheet Class 10