Solve Word Problems with Pythagorean Theorem Made Easy
Unlocking the Power of the Pythagorean Theorem
The Pythagorean theorem is a fundamental concept in geometry that has been a cornerstone of mathematics for centuries. It is a simple yet powerful tool for solving problems involving right-angled triangles. In this article, we will explore the Pythagorean theorem in depth, learn how to apply it to solve word problems, and discover its numerous real-world applications.
What is the Pythagorean Theorem?
The Pythagorean theorem is a mathematical concept that describes the relationship between the lengths of the sides of a right-angled triangle. The theorem states that:
a^2 + b^2 = c^2
where:
- a and b are the lengths of the two sides that form the right angle (the legs of the triangle)
- c is the length of the hypotenuse (the side opposite the right angle)
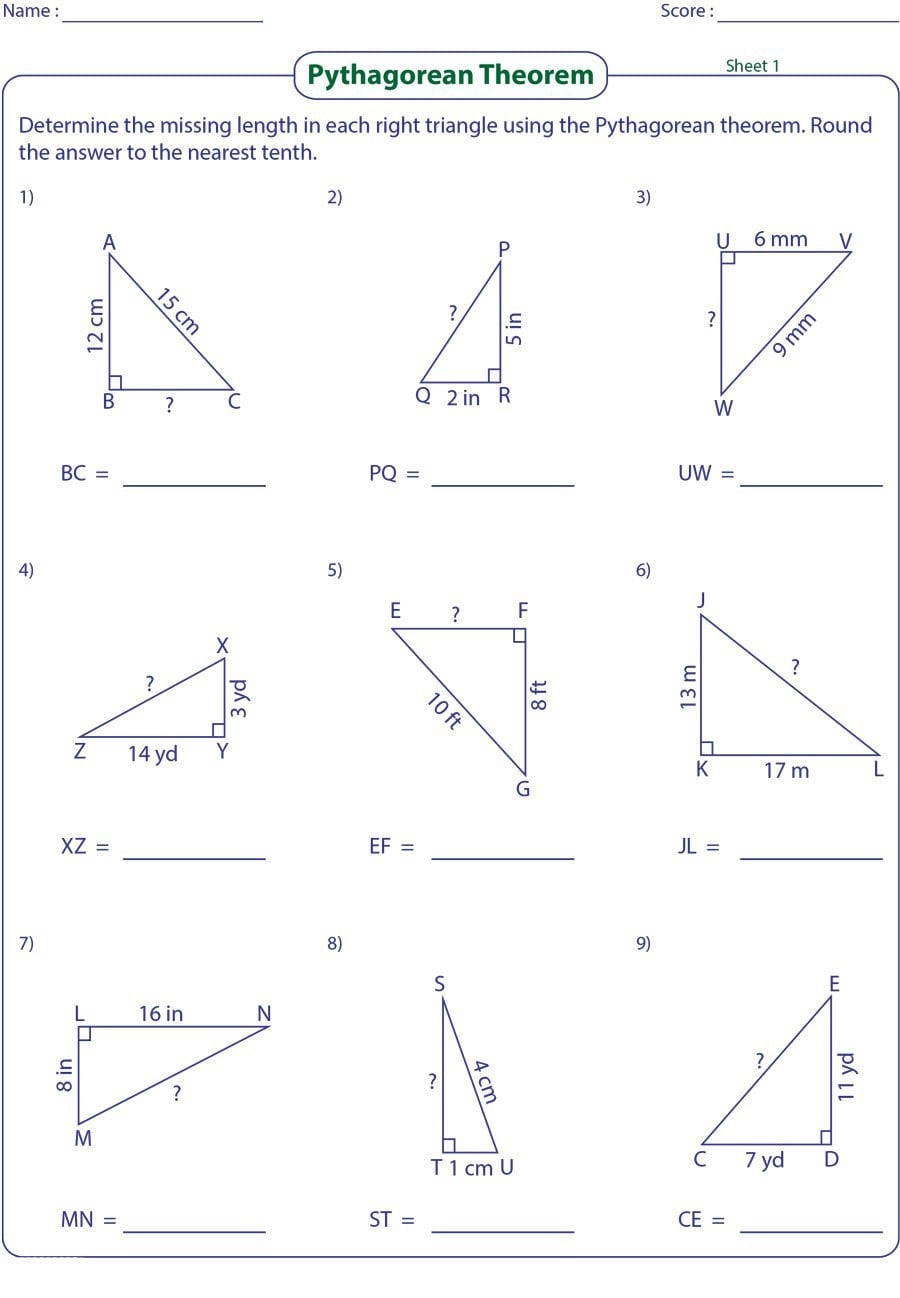
How to Apply the Pythagorean Theorem
The Pythagorean theorem can be applied in a variety of ways to solve word problems. Here are the general steps:
- Read the problem carefully: Identify the problem and understand what is being asked. Make sure you have all the necessary information.
- Draw a diagram: Draw a diagram of the situation to help visualize the problem.
- Identify the right triangle: Identify the right triangle in the diagram and label the sides.
- Plug in the values: Plug the values into the Pythagorean theorem equation (a^2 + b^2 = c^2).
- Solve for the unknown: Solve for the unknown value.
Examples of Word Problems
Here are some examples of word problems that can be solved using the Pythagorean theorem:
Example 1: Finding the Length of a Shadow
A tree is 12 meters tall, and its shadow is 5 meters long. How long is the distance from the top of the tree to the end of the shadow?
Solution:
- Draw a diagram of the situation
- Identify the right triangle (the tree, the shadow, and the distance from the top of the tree to the end of the shadow)
- Plug in the values: a = 12, b = 5, c =?
- Solve for c: c^2 = 12^2 + 5^2 = 144 + 25 = 169
- c = √169 = 13 meters
Example 2: Finding the Height of a Building
A building is 20 meters tall, and a ladder is leaning against it. The ladder is 10 meters long, and its foot is 4 meters away from the base of the building. How high up the building does the ladder reach?
Solution:
- Draw a diagram of the situation
- Identify the right triangle (the ladder, the building, and the distance from the foot of the ladder to the base of the building)
- Plug in the values: a = 10, b = 4, c =?
- Solve for c: c^2 = 10^2 + 4^2 = 100 + 16 = 116
- c = √116 ≈ 10.77 meters
Real-World Applications of the Pythagorean Theorem
The Pythagorean theorem has numerous real-world applications in fields such as:
- Construction: Building design, bridge construction, and surveying
- Physics: Projectile motion, force calculations, and energy calculations
- Engineering: Mechanical engineering, electrical engineering, and civil engineering
- Computer Science: Computer graphics, game development, and geographic information systems
📝 Note: The Pythagorean theorem is a fundamental concept in mathematics and has numerous real-world applications. It is essential to understand the theorem and its applications to solve problems in various fields.
Conclusion
In conclusion, the Pythagorean theorem is a powerful tool for solving problems involving right-angled triangles. By understanding the theorem and its applications, you can solve a wide range of word problems and real-world problems. Remember to always read the problem carefully, draw a diagram, identify the right triangle, plug in the values, and solve for the unknown.
What is the Pythagorean theorem?
+The Pythagorean theorem is a mathematical concept that describes the relationship between the lengths of the sides of a right-angled triangle. It states that a^2 + b^2 = c^2, where a and b are the lengths of the two sides that form the right angle, and c is the length of the hypotenuse.
How do I apply the Pythagorean theorem to solve word problems?
+To apply the Pythagorean theorem, read the problem carefully, draw a diagram, identify the right triangle, plug in the values, and solve for the unknown.
What are some real-world applications of the Pythagorean theorem?
+The Pythagorean theorem has numerous real-world applications in fields such as construction, physics, engineering, and computer science.
Related Terms:
- Pythagorean Theorem problems with answers
- Pythagorean theorem Word Problems calculator