Mastering Word Equations with Worksheet 6.2 Solutions

Mastering Word Equations: A Comprehensive Guide
Word equations are a crucial part of algebra, and mastering them can be a game-changer for students. In this article, we will delve into the world of word equations, explore their significance, and provide a step-by-step guide on how to solve them. Additionally, we will provide solutions to Worksheet 6.2, a popular worksheet used to assess students’ understanding of word equations.
What are Word Equations?
Word equations, also known as verbal equations or algebraic word problems, are mathematical expressions that use words to represent unknown values or relationships between variables. These equations are commonly used to describe real-world problems, making them an essential tool for problem-solving in various fields, including physics, engineering, economics, and more.
Why are Word Equations Important?
Word equations are vital in mathematics and real-world applications because they:
- Help develop problem-solving skills
- Improve critical thinking and analytical skills
- Enhance understanding of mathematical concepts and relationships
- Prepare students for advanced math and science courses
- Are used to model real-world problems and make informed decisions
How to Solve Word Equations: A Step-by-Step Guide
Solving word equations requires a systematic approach. Here’s a step-by-step guide to help you get started:
- Read and Understand the Problem: Read the word equation carefully, and identify the unknown value or relationship.
- Identify the Variables: Determine the variables involved in the equation, and assign them letters or symbols.
- Translate the Words into Mathematical Symbols: Replace the words with mathematical symbols, such as +, -, x, or /.
- Simplify the Equation: Combine like terms, and simplify the equation.
- Solve for the Unknown: Use algebraic techniques, such as addition, subtraction, multiplication, or division, to isolate the unknown value.
- Check Your Solution: Plug your solution back into the original equation to ensure it is correct.
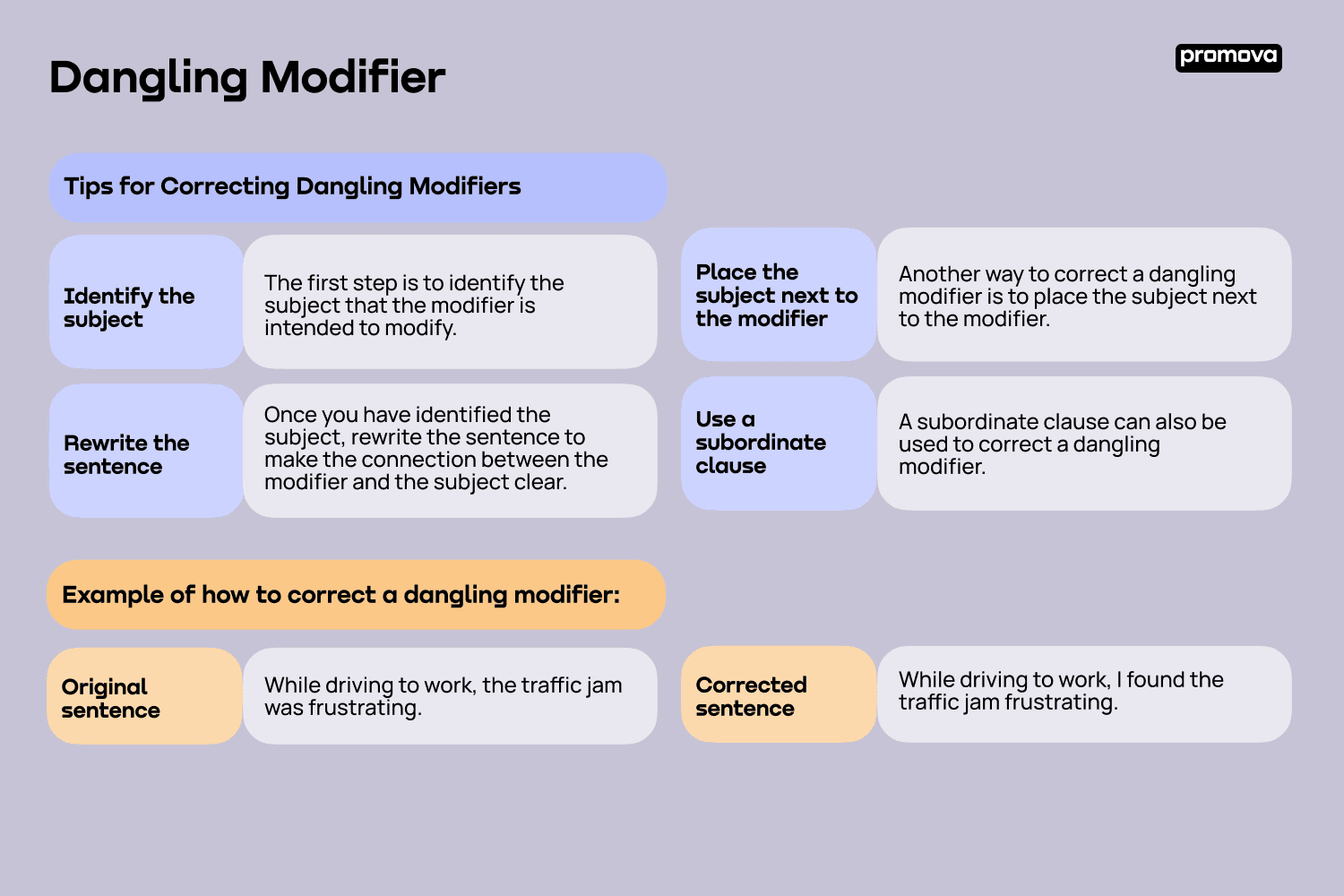
Worksheet 6.2 Solutions
Here are the solutions to Worksheet 6.2:

| Problem | Solution |
|---|---|
| 1. Tom has 15 more pencils than pens. If he has x pens, how many pencils does he have? | Let x be the number of pens. Then, the number of pencils is x + 15. |
| 2. A bookshelf has 5 shelves, and each shelf can hold 8 books. If the bookshelf is currently empty, how many books can be placed on it in total? | Let x be the total number of books. Then, x = 5 x 8 = 40. |
| 3. A bakery sells 250 loaves of bread per day. If they make a profit of $0.50 per loaf, how much profit do they make in a day? | Let x be the profit. Then, x = 250 x 0.50 = 125. |
📝 Note: Make sure to read each problem carefully and identify the unknown value or relationship before solving the equation.
Tips and Tricks for Solving Word Equations
Here are some tips and tricks to help you become a master of word equations:
- Read the problem carefully: Take your time to read the problem, and identify the unknown value or relationship.
- Use variables: Assign variables to unknown values to make the equation more manageable.
- Simplify the equation: Combine like terms, and simplify the equation to make it easier to solve.
- Check your solution: Plug your solution back into the original equation to ensure it is correct.
Conclusion
Mastering word equations requires practice, patience, and persistence. By following the step-by-step guide and tips and tricks provided in this article, you’ll become proficient in solving word equations in no time. Remember to read each problem carefully, use variables, simplify the equation, and check your solution to ensure accuracy.
What is the importance of word equations in real-world applications?
+Word equations are essential in real-world applications because they help model real-world problems, making informed decisions, and solving complex problems in various fields, including physics, engineering, economics, and more.
How do I identify the unknown value or relationship in a word equation?
+Read the problem carefully, and look for keywords such as “is,” “has,” or “more than” to identify the unknown value or relationship.
What is the difference between a word equation and a numerical equation?
+A word equation uses words to represent unknown values or relationships, while a numerical equation uses numbers and mathematical symbols to represent the relationship between variables.