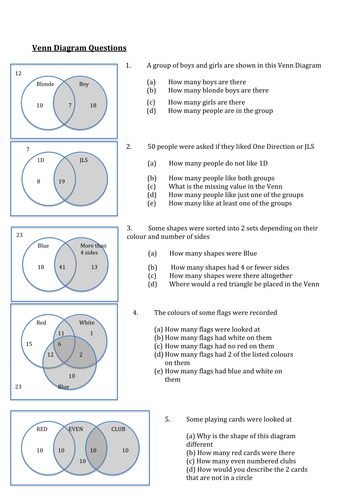
5 Ways to Master Venn Diagram Probability

Understanding the Basics of Venn Diagram Probability
Probability is a measure of the likelihood of an event occurring, and it is a fundamental concept in mathematics and statistics. One of the most effective ways to visualize and solve probability problems is by using Venn diagrams. A Venn diagram is a graphical representation of sets and their relationships, and it is a powerful tool for solving probability problems. In this article, we will explore five ways to master Venn diagram probability and become proficient in solving complex probability problems.
1. Understanding the Basics of Venn Diagrams
Before we dive into the world of probability, it is essential to understand the basics of Venn diagrams. A Venn diagram consists of overlapping circles that represent different sets. Each circle represents a set, and the overlapping region represents the intersection of the sets. The region outside the circles represents the complement of the sets.
To create a Venn diagram, you need to identify the sets and their relationships. For example, if you have two sets, A and B, you can create a Venn diagram with two overlapping circles. The region where the circles overlap represents the intersection of the sets, A ∩ B.
📝 Note: The intersection of two sets is the set of elements that are common to both sets.
2. Identifying the Types of Probability Problems
There are several types of probability problems that can be solved using Venn diagrams. Here are some of the most common types:
- Mutually Exclusive Events: Events that cannot occur simultaneously, such as rolling a 6 on a fair die and rolling an even number.
- Independent Events: Events that do not affect each other, such as flipping a coin and rolling a die.
- Dependent Events: Events that affect each other, such as drawing a card from a deck and then drawing another card.
To solve probability problems using Venn diagrams, you need to identify the type of problem and create a diagram that represents the sets and their relationships.
3. Calculating Probability Using Venn Diagrams
To calculate probability using Venn diagrams, you need to identify the favorable outcomes and the total number of outcomes. The probability of an event is equal to the number of favorable outcomes divided by the total number of outcomes.
For example, suppose you have two sets, A and B, and you want to find the probability of A ∪ B (the union of A and B). To solve this problem, you need to create a Venn diagram that represents the sets and their relationships.
| A | B | A ∩ B | A ∪ B | |
|---|---|---|---|---|
| Number of Outcomes | 10 | 15 | 5 | 20 |
In this example, the probability of A ∪ B is equal to the number of favorable outcomes (20) divided by the total number of outcomes (30).
4. Using Venn Diagrams to Solve Complex Probability Problems
Venn diagrams are particularly useful for solving complex probability problems that involve multiple sets and relationships. Here’s an example:
Suppose you have three sets, A, B, and C, and you want to find the probability of A ∩ B ∩ C (the intersection of A, B, and C). To solve this problem, you need to create a Venn diagram that represents the sets and their relationships.
| A | B | C | A ∩ B | A ∩ C | B ∩ C | A ∩ B ∩ C | |
|---|---|---|---|---|---|---|---|
| Number of Outcomes | 10 | 15 | 20 | 5 | 10 | 15 | 5 |
In this example, the probability of A ∩ B ∩ C is equal to the number of favorable outcomes (5) divided by the total number of outcomes (60).
5. Practicing with Real-World Examples
The best way to master Venn diagram probability is to practice with real-world examples. Here are a few examples to get you started:
- Medical Diagnosis: A doctor wants to know the probability that a patient has a disease given that they have a positive test result. The doctor can use a Venn diagram to represent the sets of patients with the disease and patients with a positive test result.
- Insurance: An insurance company wants to know the probability that a driver will have an accident given that they have a history of accidents. The company can use a Venn diagram to represent the sets of drivers with a history of accidents and drivers who will have an accident.
By practicing with real-world examples, you can develop your skills in using Venn diagrams to solve probability problems.
In summary, mastering Venn diagram probability requires a deep understanding of the basics of Venn diagrams, the types of probability problems, and how to calculate probability using Venn diagrams. By practicing with real-world examples, you can develop your skills in using Venn diagrams to solve complex probability problems.
What is a Venn diagram?
+A Venn diagram is a graphical representation of sets and their relationships.
What is the intersection of two sets?
+The intersection of two sets is the set of elements that are common to both sets.
How do you calculate probability using Venn diagrams?
+To calculate probability using Venn diagrams, you need to identify the favorable outcomes and the total number of outcomes, and then divide the number of favorable outcomes by the total number of outcomes.
Related Terms:
- Venn diagrams Worksheet tes
- Venn diagram Worksheet PDF
- Venn diagram probability questions
- Venn diagram conditional probability