Unit Circle Worksheet With Answers for Math Students
Understanding the Unit Circle: A Comprehensive Guide for Math Students
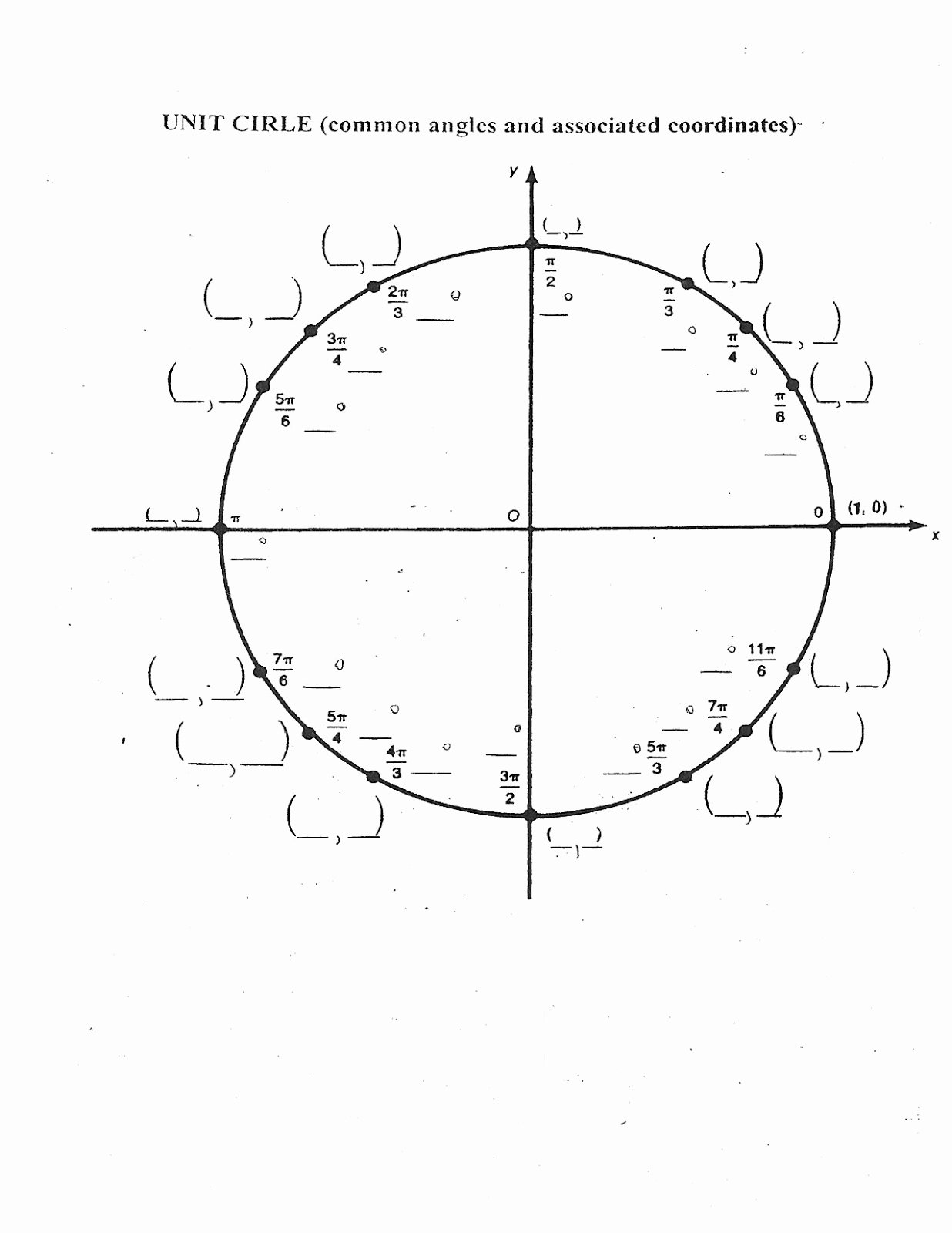
The unit circle is a fundamental concept in mathematics, particularly in trigonometry and geometry. It is a circle with a radius of 1 unit, centered at the origin of the coordinate plane. The unit circle is used to define the trigonometric functions, such as sine, cosine, and tangent, and is essential for solving problems involving right triangles and circular motion.
Key Components of the Unit Circle
The unit circle has several key components that are crucial for understanding its properties and applications.
- Radius: The radius of the unit circle is 1 unit, which is the distance from the center of the circle to any point on the circle.
- Center: The center of the unit circle is at the origin (0, 0) of the coordinate plane.
- Circumference: The circumference of the unit circle is 2π units, which is the distance around the circle.
- Angles: The unit circle is divided into 360 degrees, with each degree representing a central angle of the circle.
Trigonometric Functions on the Unit Circle
The unit circle is used to define the trigonometric functions, including sine, cosine, and tangent. These functions relate the angles of the unit circle to the ratios of the sides of right triangles.
- Sine: The sine of an angle is defined as the ratio of the opposite side to the hypotenuse of a right triangle.
- Cosine: The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse of a right triangle.
- Tangent: The tangent of an angle is defined as the ratio of the opposite side to the adjacent side of a right triangle.
Unit Circle Worksheet
Here is a worksheet with answers to help you practice working with the unit circle:
Section 1: Multiple Choice Questions
- What is the radius of the unit circle? a) 1 unit b) 2 units c) 3 units d) 4 units
Answer: a) 1 unit
- What is the center of the unit circle? a) (0, 0) b) (1, 0) c) (0, 1) d) (1, 1)
Answer: a) (0, 0)
- What is the circumference of the unit circle? a) π units b) 2π units c) 3π units d) 4π units
Answer: b) 2π units
Section 2: Short Answer Questions
- What is the sine of 30° on the unit circle?
Answer: The sine of 30° is 1⁄2.
- What is the cosine of 45° on the unit circle?
Answer: The cosine of 45° is 1/√2.
- What is the tangent of 60° on the unit circle?
Answer: The tangent of 60° is √3.
Section 3: Problems
- Find the value of sin(θ) on the unit circle, given that θ = 60°.
Answer: sin(60°) = √3/2
- Find the value of cos(θ) on the unit circle, given that θ = 30°.
Answer: cos(30°) = √3/2
- Find the value of tan(θ) on the unit circle, given that θ = 45°.
Answer: tan(45°) = 1
📝 Note: Make sure to show your work and use the unit circle to find the values of the trigonometric functions.
Section 4: True or False Questions
The unit circle has a radius of 2 units. (False)
The center of the unit circle is at (1, 0). (False)
The circumference of the unit circle is π units. (False)
Conclusion
The unit circle is a fundamental concept in mathematics that is used to define the trigonometric functions and solve problems involving right triangles and circular motion. By understanding the key components of the unit circle, including the radius, center, and circumference, you can develop a strong foundation in trigonometry and geometry.
What is the unit circle?
+The unit circle is a circle with a radius of 1 unit, centered at the origin of the coordinate plane.
What are the key components of the unit circle?
+The key components of the unit circle are the radius, center, and circumference.
What is the sine of 30° on the unit circle?
+The sine of 30° is 1⁄2.
Related Terms:
- Unit circle worksheet pdf
- Trig unit circle Worksheet pdf
- Unit Circle Worksheet answer Key
- Unit Circle Worksheet pdf Kuta