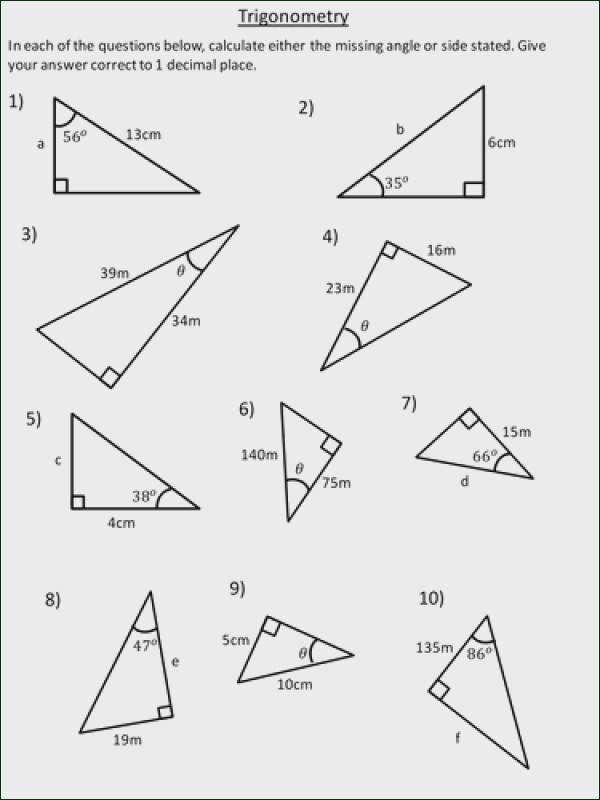
Mastering Trig Ratios Worksheet for Math Success

Unlocking the Secrets of Trigonometric Ratios for Academic Excellence
Trigonometry, a branch of mathematics that deals with the relationships between the sides and angles of triangles, is a fundamental concept that has numerous applications in various fields such as physics, engineering, and computer science. One of the most crucial aspects of trigonometry is understanding trigonometric ratios, which are essential for solving problems involving right-angled triangles. In this article, we will delve into the world of trig ratios, exploring their definitions, applications, and providing a comprehensive worksheet to help students master these concepts.
Understanding Trigonometric Ratios
Trigonometric ratios, also known as trig ratios, are relationships between the lengths of the sides of a right-angled triangle. These ratios are used to describe the angles of a triangle and are defined as follows:
- Sine (sin): The ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan): The ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
These ratios can be represented mathematically as:
| Trigonometric Ratio | Formula |
|---|---|
| Sine (sin) | sin(A) = opposite side / hypotenuse |
| Cosine (cos) | cos(A) = adjacent side / hypotenuse |
| Tangent (tan) | tan(A) = opposite side / adjacent side |
Applications of Trigonometric Ratios
Trigonometric ratios have numerous applications in various fields, including:
- Physics: Trigonometric ratios are used to describe the motion of objects, forces, and energies.
- Engineering: Trigonometric ratios are used in the design of buildings, bridges, and other structures.
- Computer Science: Trigonometric ratios are used in computer graphics, game development, and scientific simulations.
Mastering Trigonometric Ratios with a Worksheet
To help students master trigonometric ratios, we have created a comprehensive worksheet that covers the basics of trig ratios, their applications, and problem-solving exercises.
Worksheet: Trigonometric Ratios
Section 1: Multiple Choice Questions
- What is the sine of an angle in a right-angled triangle? a) opposite side / hypotenuse b) adjacent side / hypotenuse c) opposite side / adjacent side d) hypotenuse / opposite side
Answer: a) opposite side / hypotenuse
- Which trigonometric ratio is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle? a) Sine (sin) b) Cosine (cos) c) Tangent (tan) d) Cotangent (cot)
Answer: c) Tangent (tan)
Section 2: Short Answer Questions
- What is the cosine of an angle in a right-angled triangle?
Answer: _______________________
- What is the tangent of an angle in a right-angled triangle?
Answer: _______________________
Section 3: Problem-Solving Exercises
- In a right-angled triangle, the length of the hypotenuse is 10 cm and the length of the side opposite the angle is 6 cm. What is the sine of the angle?
Answer: _______________________
- In a right-angled triangle, the length of the side adjacent to the angle is 8 cm and the length of the side opposite the angle is 6 cm. What is the tangent of the angle?
Answer: _______________________
💡 Note: Use the formulas and definitions of trigonometric ratios to solve the problems.
Section 4: Word Problems
- A building is 50 meters tall, and the angle of elevation to the top of the building is 30°. What is the distance from the point of observation to the building?
Answer: _______________________
- A car is traveling at a speed of 60 km/h, and the angle of elevation to the top of a hill is 20°. What is the height of the hill?
Answer: _______________________
📝 Note: Use the trigonometric ratios to solve the word problems.
Conclusion
Mastering trigonometric ratios is essential for academic success in mathematics and science. With this worksheet, students can practice and reinforce their understanding of trig ratios and their applications. By solving the multiple-choice questions, short answer questions, problem-solving exercises, and word problems, students can develop a deeper understanding of trigonometric ratios and improve their problem-solving skills.
What are the three main trigonometric ratios?
+The three main trigonometric ratios are sine (sin), cosine (cos), and tangent (tan).
What is the sine of an angle in a right-angled triangle?
+The sine of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
What is the tangent of an angle in a right-angled triangle?
+The tangent of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Related Terms:
- Hipotenusa
- Trigonometri
- Segitiga
- Geometri
- Logaritma
- Fungsi trigonometri