5 Ways to Master Rotation 90 Degrees Counterclockwise

Understanding Rotation 90 Degrees Counterclockwise

Rotation 90 degrees counterclockwise is a fundamental concept in mathematics, particularly in geometry and trigonometry. It involves rotating a shape or an object 90 degrees in a counterclockwise direction, which can be a bit tricky to visualize and master. However, with practice and the right strategies, anyone can become proficient in rotation 90 degrees counterclockwise. In this article, we will explore five ways to master this concept.

Method 1: Using Coordinate Grids

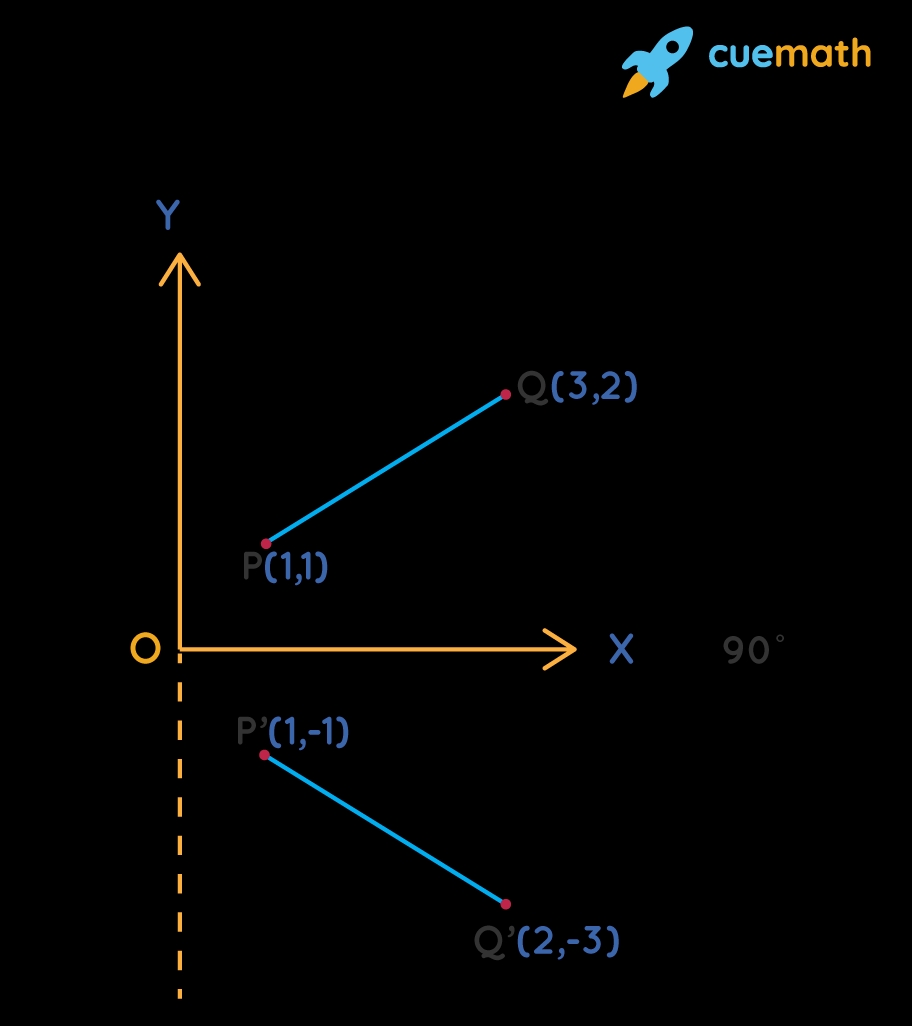
One effective way to master rotation 90 degrees counterclockwise is by using coordinate grids. A coordinate grid is a graphical representation of a two-dimensional plane, where each point is represented by a pair of coordinates (x, y). When rotating a shape 90 degrees counterclockwise, the x and y coordinates of each point are swapped, and the new x coordinate becomes the negative of the original y coordinate.

For example, if we have a point (3, 4) on a coordinate grid, its image after rotating 90 degrees counterclockwise would be (-4, 3). By using coordinate grids, you can visualize and practice rotation 90 degrees counterclockwise with ease.

Key Takeaways:

• To rotate a point 90 degrees counterclockwise, swap the x and y coordinates and make the new x coordinate negative.
• Use a coordinate grid to visualize and practice rotation 90 degrees counterclockwise.

📝 Note: Practice rotating different shapes and objects on a coordinate grid to become more comfortable with this method.

Method 2: Visualizing with a Clock Analogy

Another way to master rotation 90 degrees counterclockwise is by using a clock analogy. Imagine a clock with the 12 o’clock position at the top. When rotating a shape 90 degrees counterclockwise, it’s like moving the clock hand from the 12 o’clock position to the 9 o’clock position.

This analogy can help you visualize the rotation more easily, especially when dealing with complex shapes or objects. By imagining the clock hand moving in a counterclockwise direction, you can better understand the rotation and its effect on the shape or object.

Key Takeaways:

• Use a clock analogy to visualize rotation 90 degrees counterclockwise.
• Imagine the clock hand moving from the 12 o’clock position to the 9 o’clock position.

🕰️ Note: Practice using the clock analogy with different shapes and objects to improve your visualization skills.

Method 3: Using Geometry Software

Geometry software can be a powerful tool for mastering rotation 90 degrees counterclockwise. Programs like GeoGebra or Geometer’s Sketchpad allow you to create and manipulate geometric shapes, including rotating them 90 degrees counterclockwise.

By using geometry software, you can explore and experiment with different shapes and rotations, making it easier to understand and visualize the concept. Additionally, these programs often provide interactive tools and features that can help you develop a deeper understanding of rotation 90 degrees counterclockwise.

Key Takeaways:

• Use geometry software to explore and experiment with rotation 90 degrees counterclockwise.
• Take advantage of interactive tools and features to develop a deeper understanding of the concept.

💻 Note: Experiment with different geometry software programs to find the one that works best for you.

Method 4: Practicing with Real-World Objects

Practicing with real-world objects is another effective way to master rotation 90 degrees counterclockwise. By using everyday objects, such as a book or a pencil, you can visualize and practice rotation 90 degrees counterclockwise in a more tangible way.

For example, imagine rotating a book 90 degrees counterclockwise. You can visualize the book’s cover and pages moving in a counterclockwise direction, making it easier to understand the rotation.

Key Takeaways:

• Use real-world objects to practice and visualize rotation 90 degrees counterclockwise.
• Experiment with different objects to develop a deeper understanding of the concept.

📚 Note: Practice rotating different objects in different directions to improve your understanding of rotation 90 degrees counterclockwise.

Method 5: Breaking Down Complex Shapes

Finally, breaking down complex shapes into simpler components can help you master rotation 90 degrees counterclockwise. By identifying the individual parts of a shape and rotating each part separately, you can better understand the overall rotation.

For example, imagine rotating a complex shape like a hexagon 90 degrees counterclockwise. By breaking down the hexagon into individual triangles and rotating each triangle separately, you can visualize and understand the overall rotation more easily.

Key Takeaways:

• Break down complex shapes into simpler components to understand rotation 90 degrees counterclockwise.
• Identify individual parts of a shape and rotate each part separately.

🔍 Note: Practice breaking down different shapes to develop a deeper understanding of rotation 90 degrees counterclockwise.

In conclusion, mastering rotation 90 degrees counterclockwise requires practice, patience, and the right strategies. By using coordinate grids, visualizing with a clock analogy, using geometry software, practicing with real-world objects, and breaking down complex shapes, you can develop a deeper understanding of this fundamental concept. With consistent practice and application, you can become proficient in rotation 90 degrees counterclockwise and improve your overall math skills.