7 Ways to Master Graphing Sine and Cosine Functions
Unlocking the Secrets of Sine and Cosine Functions
Graphing sine and cosine functions can be a daunting task for many students, but with the right strategies and techniques, anyone can master these essential trigonometric functions. In this article, we will explore seven ways to help you improve your skills in graphing sine and cosine functions.
Understanding the Basics
Before we dive into the strategies, it’s essential to review the basics of sine and cosine functions. Both functions are periodic, meaning they repeat their values at regular intervals. The sine function is an odd function, while the cosine function is an even function. This means that the sine function satisfies the condition sin(-x) = -sin(x), while the cosine function satisfies the condition cos(-x) = cos(x).
1. Learn the Unit Circle
The unit circle is a fundamental concept in trigonometry, and it’s essential to understand it when graphing sine and cosine functions. The unit circle is a circle with a radius of 1, centered at the origin of the coordinate plane. By using the unit circle, you can visualize the values of sine and cosine for different angles.

| Angle (in degrees) | Sine Value | Cosine Value |
|---|---|---|
| 0° | 0 | 1 |
| 30° | 1/2 | √3/2 |
| 45° | 1/√2 | 1/√2 |
| 60° | √3/2 | 1/2 |
| 90° | 1 | 0 |
📝 Note: The unit circle is a powerful tool for visualizing the relationships between angles and trigonometric values. Make sure to practice using it to improve your understanding of sine and cosine functions.
2. Identify the Period and Amplitude
When graphing sine and cosine functions, it’s essential to identify the period and amplitude. The period is the distance along the x-axis over which the function repeats itself, while the amplitude is the maximum value of the function.
- The period of the sine function is 2π, while the period of the cosine function is also 2π.
- The amplitude of the sine function is 1, while the amplitude of the cosine function is also 1.
📝 Note: Understanding the period and amplitude of sine and cosine functions will help you graph them more accurately.
3. Use the Five-Point Method
The five-point method is a technique for graphing sine and cosine functions quickly and accurately. To use this method, follow these steps:
- Identify the period and amplitude of the function.
- Plot the points at x = 0, π/2, π, 3π/2, and 2π.
- Connect the points with a smooth curve.
📝 Note: The five-point method is a useful technique for graphing sine and cosine functions, but it's essential to practice using it to become proficient.
4. Graph the Basic Functions
To master graphing sine and cosine functions, it’s essential to practice graphing the basic functions:
- y = sin(x)
- y = cos(x)
Start by graphing these functions on the same coordinate plane to visualize their relationships.
📝 Note: Graphing the basic functions will help you understand the relationships between sine and cosine functions.
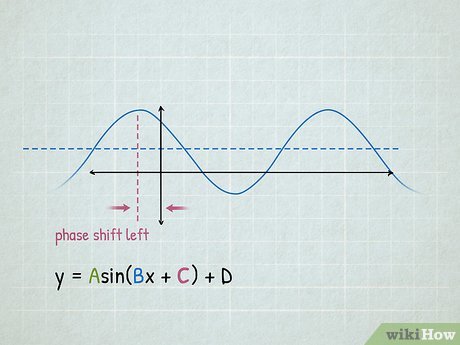
5. Learn to Shift and Reflect the Functions
To graph more complex sine and cosine functions, you need to learn how to shift and reflect the basic functions. For example:
- To shift the sine function to the right by π/2 units, use the equation y = sin(x - π/2).
- To reflect the cosine function across the x-axis, use the equation y = -cos(x).
📝 Note: Understanding how to shift and reflect sine and cosine functions will help you graph more complex functions.
6. Practice, Practice, Practice!
To master graphing sine and cosine functions, it’s essential to practice regularly. Start with simple functions and gradually move on to more complex ones. Use online graphing tools or software to visualize the functions and check your work.
📝 Note: Practice is key to mastering graphing sine and cosine functions. Make sure to practice regularly to become proficient.
7. Use Real-World Applications
Finally, try to use real-world applications to make graphing sine and cosine functions more meaningful. For example, you can use these functions to model sound waves, light waves, or ocean tides.
📝 Note: Using real-world applications will help you see the relevance of graphing sine and cosine functions in real-life situations.
To recap, mastering graphing sine and cosine functions requires a combination of understanding the basics, learning the unit circle, identifying the period and amplitude, using the five-point method, graphing the basic functions, shifting and reflecting the functions, practicing regularly, and using real-world applications. By following these seven strategies, you’ll become proficient in graphing sine and cosine functions in no time.
What is the unit circle?
+The unit circle is a circle with a radius of 1, centered at the origin of the coordinate plane. It’s a fundamental concept in trigonometry and helps visualize the values of sine and cosine for different angles.
How do I identify the period and amplitude of a sine or cosine function?
+The period of a sine or cosine function is the distance along the x-axis over which the function repeats itself. The amplitude is the maximum value of the function. For example, the period of the sine function is 2π, and the amplitude is 1.
What is the five-point method for graphing sine and cosine functions?
+The five-point method is a technique for graphing sine and cosine functions quickly and accurately. It involves identifying the period and amplitude of the function, plotting five key points, and connecting them with a smooth curve.