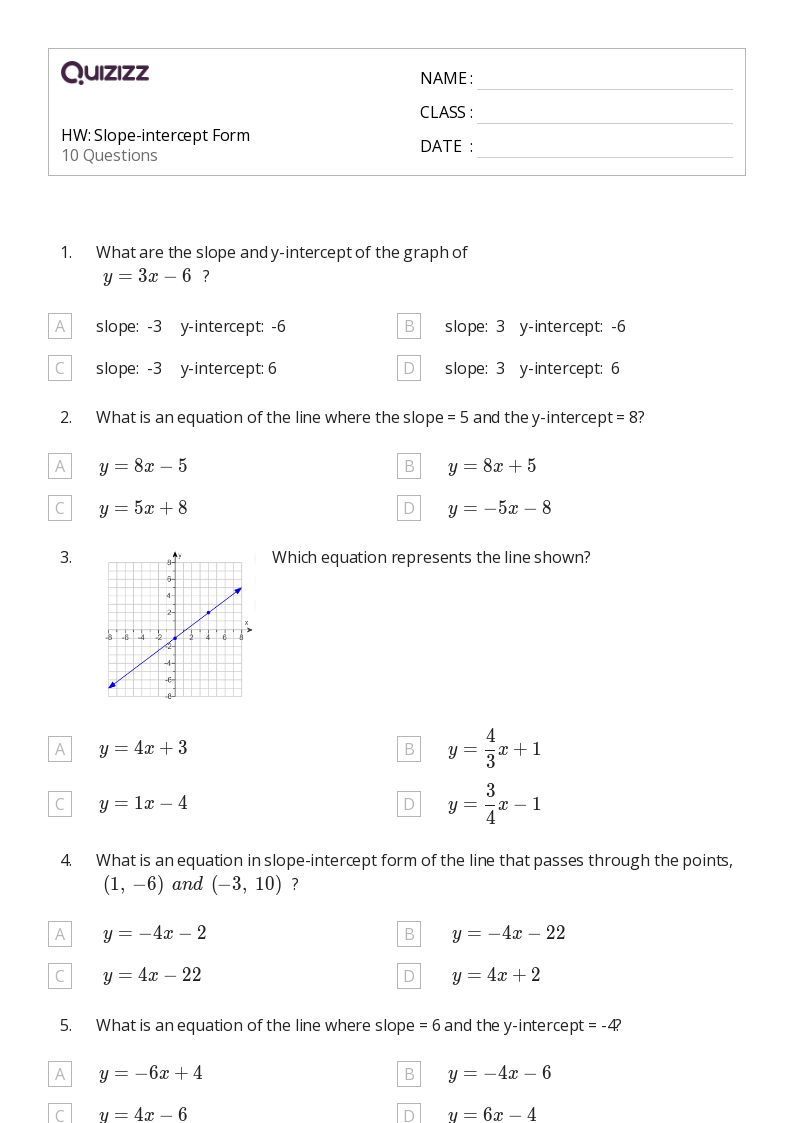
5 Ways to Master Rational Exponents

Understanding Rational Exponents
Rational exponents can be intimidating, but with the right approach, you can master them. Rational exponents are a way of expressing radicals using exponent notation. They are called rational because they involve fractions. In this blog post, we will explore five ways to master rational exponents, making it easier for you to work with them.
1. Reviewing the Basics of Exponents
Before diving into rational exponents, it’s essential to review the basics of exponents. Exponents are shorthand for repeated multiplication. For example, 2³ means 2 × 2 × 2. Understanding the rules of exponents, such as the product rule, quotient rule, and power rule, will help you to understand rational exponents better.
Rules of Exponents:
- Product Rule: aᵐ × aⁿ = aᵐ⁺ⁿ
- Quotient Rule: aᵐ ÷ aⁿ = aᵐ⁻ⁿ
- Power Rule: (aᵐ)ⁿ = aᵐⁿ
2. Understanding the Concept of Rational Exponents
Rational exponents are a way of expressing radicals using exponent notation. A rational exponent is an exponent that is a fraction. For example, 2¹/² is a rational exponent. This can be rewritten as √2. Understanding the relationship between radicals and rational exponents is crucial to mastering rational exponents.
Relationship between Radicals and Rational Exponents:
- aᵐ/ⁿ = (aᵐ)¹/ⁿ = √ⁿ(aᵐ)
- aᵐ/ⁿ = aᵐ × a¹/ⁿ
3. Simplifying Rational Exponents
Simplifying rational exponents involves rewriting them in a simpler form. This can be done by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
Simplifying Rational Exponents:
- 2³/⁴ = 2³ × 2⁻¹ = 2²
- 3⁵/⁶ = 3⁵ × 3⁻¹ = 3⁴
4. Multiplying and Dividing Rational Exponents
Multiplying and dividing rational exponents involves applying the rules of exponents.
Multiplying and Dividing Rational Exponents:
- 2¹/² × 2³/⁴ = 2¹/² + ³/⁴ = 2⁴/⁶ = 2²/³
- 3²/³ ÷ 3¹/² = 3²/³ - ¹/² = 3¹/⁶ = 3¹/⁶
5. Applying Rational Exponents to Real-World Problems
Rational exponents have many real-world applications, such as finance, physics, and engineering. Applying rational exponents to real-world problems will help you to understand their practical significance.
Real-World Applications of Rational Exponents:
- Finance: Rational exponents can be used to calculate compound interest rates.
- Physics: Rational exponents can be used to calculate the velocity of an object.
- Engineering: Rational exponents can be used to calculate the stress on a beam.
🤔 Note: Rational exponents are used in many mathematical formulas, so it's essential to understand how to work with them.
To summarize, mastering rational exponents requires a solid understanding of the basics of exponents, the concept of rational exponents, simplifying rational exponents, multiplying and dividing rational exponents, and applying rational exponents to real-world problems. By following these steps, you can become proficient in working with rational exponents.
What is a rational exponent?
+A rational exponent is an exponent that is a fraction.
How do you simplify rational exponents?
+Simplifying rational exponents involves rewriting them in a simpler form by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
What are some real-world applications of rational exponents?
+Rational exponents have many real-world applications, such as finance, physics, and engineering.