Pythagorean Theorem Worksheet for Math Success

Unlocking Math Success: A Comprehensive Guide to the Pythagorean Theorem
Mathematics is an essential part of our daily lives, and mastering its concepts is crucial for problem-solving and critical thinking. Among the numerous mathematical theories and formulas, the Pythagorean Theorem stands out as a fundamental concept in geometry and trigonometry. In this article, we will delve into the world of the Pythagorean Theorem, exploring its history, significance, and practical applications.
What is the Pythagorean Theorem?
The Pythagorean Theorem is a mathematical formula that describes the relationship between the lengths of the sides of a right-angled triangle. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, this can be expressed as:
a² + b² = c²
where:
- a is the length of one side (leg)
- b is the length of the other side (leg)
- c is the length of the hypotenuse
History of the Pythagorean Theorem
The Pythagorean Theorem has a rich history that dates back to ancient civilizations. Although it is named after the Greek philosopher and mathematician Pythagoras, the theorem was known and used by other cultures before him. The ancient Egyptians, Babylonians, and Chinese all used the theorem in their mathematical and architectural endeavors.
The theorem was first proven by Pythagoras in the 6th century BCE, and it was later popularized by the Greek mathematician Euclid in his book “Elements.” Since then, the Pythagorean Theorem has become a cornerstone of mathematics and has been widely used in various fields, including physics, engineering, and architecture.
Significance of the Pythagorean Theorem
The Pythagorean Theorem is a fundamental concept in mathematics, and its significance extends beyond the realm of geometry and trigonometry. Here are a few reasons why the theorem is so important:
- Problem-solving: The Pythagorean Theorem provides a powerful tool for solving problems involving right-angled triangles.
- Distance calculations: The theorem can be used to calculate distances and heights in various fields, such as physics, engineering, and architecture.
- Mathematical modeling: The Pythagorean Theorem is used to model real-world situations, such as the trajectory of projectiles and the design of buildings.
- Critical thinking: The theorem promotes critical thinking and problem-solving skills, essential for mathematics and other subjects.
Practical Applications of the Pythagorean Theorem
The Pythagorean Theorem has numerous practical applications in various fields. Here are a few examples:
- Physics: The theorem is used to calculate distances, velocities, and accelerations in problems involving motion.
- Engineering: The theorem is used in the design of buildings, bridges, and other structures to calculate stresses and loads.
- Architecture: The theorem is used to calculate distances and heights in building design and construction.
- Computer graphics: The theorem is used to create 3D models and animations.
How to Use the Pythagorean Theorem
Using the Pythagorean Theorem is straightforward. Here are the steps:
- Identify the right-angled triangle and label the sides.
- Plug the values of the sides into the formula: a² + b² = c²
- Solve for the unknown side.
For example, if you have a right-angled triangle with one side measuring 3 inches and the other side measuring 4 inches, you can use the theorem to calculate the length of the hypotenuse:
3² + 4² = c² 9 + 16 = c² 25 = c² c = √25 c = 5 inches
📝 Note: The Pythagorean Theorem only works for right-angled triangles. If the triangle is not right-angled, you will need to use other formulas or techniques to solve the problem.
Pythagorean Theorem Worksheet
Practice makes perfect! Here are a few practice questions to help you master the Pythagorean Theorem:
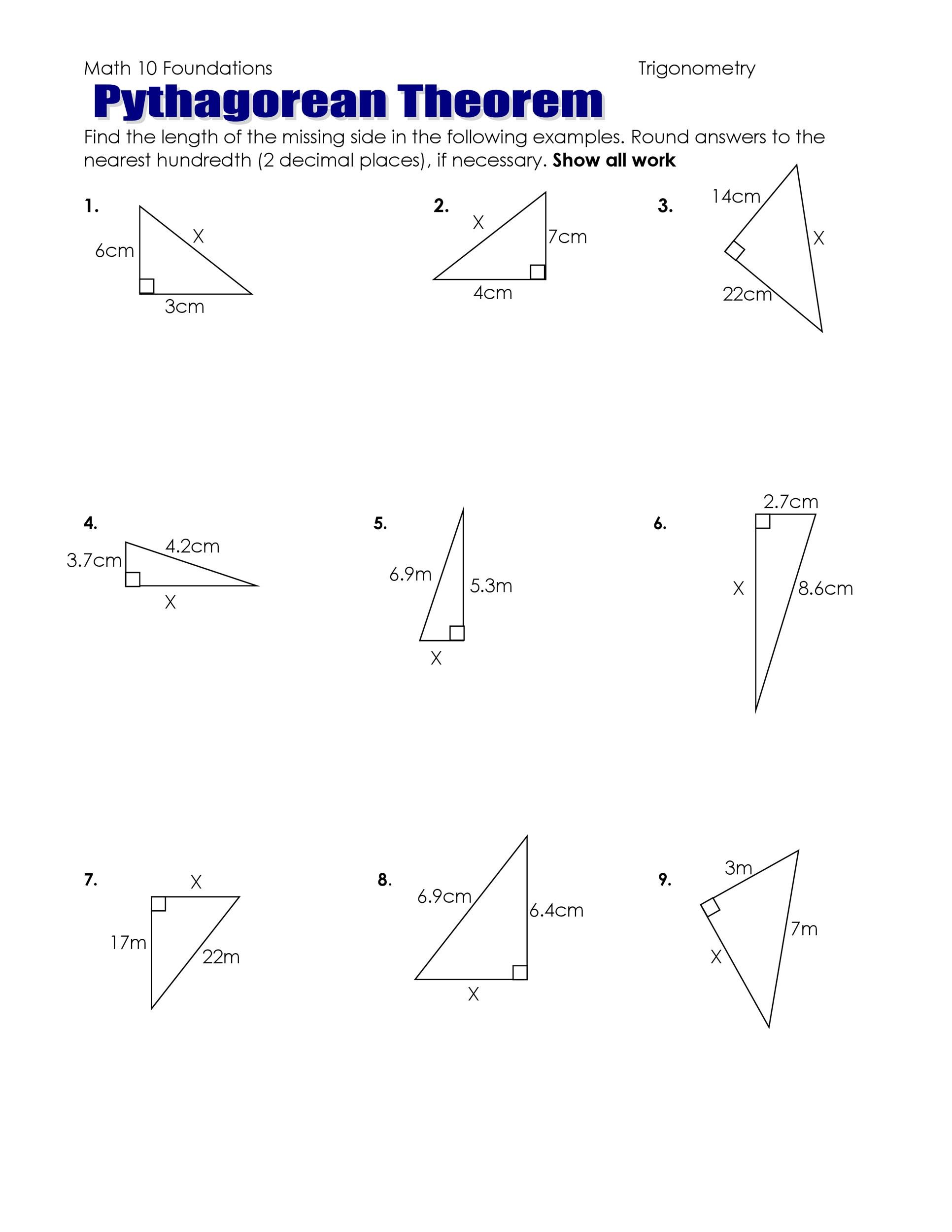
| Problem | a | b | c |
|---|---|---|---|
| 1 | 3 | 4 | ? |
| 2 | 5 | 12 | ? |
| 3 | 8 | 15 | ? |
| 4 | 10 | 24 | ? |
| 5 | 7 | 9 | ? |
Solutions:
| Problem | Solution |
|---|---|
| 1 | c = 5 inches |
| 2 | c = 13 inches |
| 3 | c = 17 inches |
| 4 | c = 26 inches |
| 5 | c = 11.3 inches |
Conclusion
The Pythagorean Theorem is a fundamental concept in mathematics that has far-reaching applications in various fields. By understanding and applying the theorem, you can solve problems involving right-angled triangles and develop critical thinking and problem-solving skills. Remember to practice regularly and use the theorem to solve real-world problems.
What is the Pythagorean Theorem?
+The Pythagorean Theorem is a mathematical formula that describes the relationship between the lengths of the sides of a right-angled triangle.
How do I use the Pythagorean Theorem?
+Identify the right-angled triangle, label the sides, and plug the values into the formula: a² + b² = c². Solve for the unknown side.
What are some practical applications of the Pythagorean Theorem?
+The theorem has numerous practical applications in physics, engineering, architecture, and computer graphics.