5 Ways to Solve Systems of Equations by Graphing
Introduction to Solving Systems of Equations by Graphing
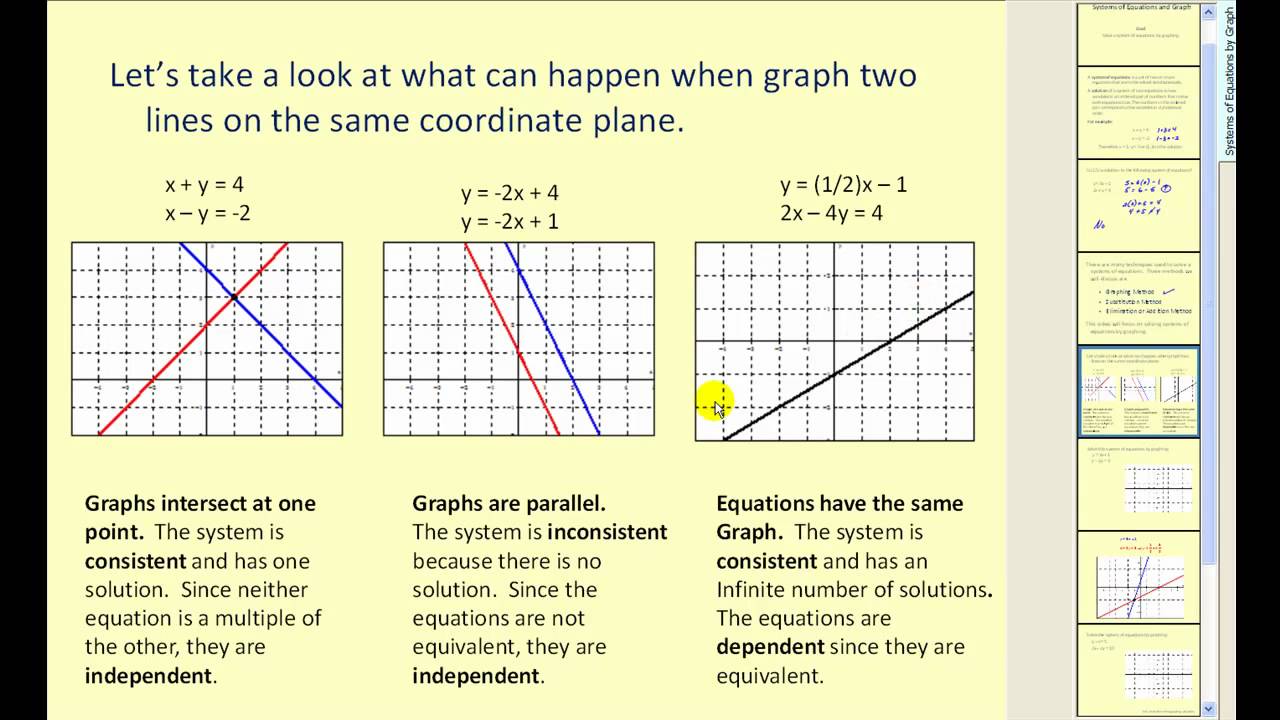
Solving systems of equations is a fundamental concept in mathematics, and one of the most effective methods is graphing. Graphing involves representing the equations on a coordinate plane and finding the point of intersection, which represents the solution. In this blog post, we will explore five ways to solve systems of equations by graphing.
Understanding the Basics of Graphing
Before we dive into the methods, it’s essential to understand the basics of graphing. Graphing involves representing equations on a coordinate plane, where the x-axis represents the independent variable and the y-axis represents the dependent variable. The point of intersection between two lines represents the solution to the system of equations.
Method 1: Graphing Linear Equations
One of the simplest methods of solving systems of equations by graphing is by graphing linear equations. Linear equations are represented by a straight line on the coordinate plane. To solve a system of linear equations, simply graph both equations on the same coordinate plane and find the point of intersection.
For example, consider the following system of equations:
2x + 3y = 7 x - 2y = -3
To solve this system, graph both equations on the same coordinate plane.
📝 Note: Make sure to label the x and y axes correctly and use a ruler to draw the lines accurately.
The point of intersection represents the solution to the system.
Method 2: Graphing Quadratic Equations
Graphing quadratic equations is slightly more complex than graphing linear equations. Quadratic equations are represented by a parabola on the coordinate plane. To solve a system of quadratic equations, graph both equations on the same coordinate plane and find the point of intersection.
For example, consider the following system of equations:
x^2 + 4y^2 = 16 x^2 - 2y^2 = 4
To solve this system, graph both equations on the same coordinate plane.
📝 Note: Use a calculator or software to graph the parabolas accurately.
The point of intersection represents the solution to the system.
Method 3: Graphing Systems with Inequalities
Graphing systems with inequalities involves representing the inequalities on a coordinate plane and finding the region of intersection. To solve a system with inequalities, graph both inequalities on the same coordinate plane and shade the region of intersection.
For example, consider the following system:
2x + 3y ≥ 7 x - 2y ≤ -3
To solve this system, graph both inequalities on the same coordinate plane.
📝 Note: Use a solid line for ≥ and ≤ inequalities and a dashed line for < and > inequalities.
The region of intersection represents the solution to the system.
Method 4: Graphing Systems with Circle Equations
Graphing systems with circle equations involves representing the circle equations on a coordinate plane and finding the point of intersection. To solve a system with circle equations, graph both equations on the same coordinate plane.
For example, consider the following system:
(x - 2)^2 + (y - 3)^2 = 16 (x + 1)^2 + (y - 2)^2 = 9
To solve this system, graph both equations on the same coordinate plane.
📝 Note: Use a calculator or software to graph the circles accurately.
The point of intersection represents the solution to the system.
Method 5: Graphing Systems with Parametric Equations
Graphing systems with parametric equations involves representing the parametric equations on a coordinate plane and finding the point of intersection. To solve a system with parametric equations, graph both equations on the same coordinate plane.
For example, consider the following system:
x = 2t + 1 y = -3t + 2 x = t^2 + 1 y = 2t - 1
To solve this system, graph both equations on the same coordinate plane.
📝 Note: Use a calculator or software to graph the parametric equations accurately.
The point of intersection represents the solution to the system.
Wrapping Up
In this blog post, we explored five ways to solve systems of equations by graphing. From graphing linear equations to graphing systems with parametric equations, we covered a range of methods to help you solve systems of equations with ease. Remember to always label the x and y axes correctly, use a ruler to draw the lines accurately, and use a calculator or software to graph the equations accurately.
What is the best method for solving systems of equations by graphing?
+
The best method for solving systems of equations by graphing depends on the type of equations involved. For linear equations, graphing is a straightforward method. For quadratic equations, graphing is more complex but still effective. For systems with inequalities, graphing involves shading the region of intersection. For systems with circle equations, graphing involves finding the point of intersection. For systems with parametric equations, graphing involves finding the point of intersection.
What are the benefits of solving systems of equations by graphing?
+
Solving systems of equations by graphing has several benefits. It allows for a visual representation of the equations, making it easier to understand the relationships between the variables. It also provides a way to check the solution, as the point of intersection represents the solution. Additionally, graphing can help identify the type of solution, such as a single solution, no solution, or infinitely many solutions.
What are some common mistakes to avoid when solving systems of equations by graphing?
+
Some common mistakes to avoid when solving systems of equations by graphing include not labeling the x and y axes correctly, not using a ruler to draw the lines accurately, and not using a calculator or software to graph the equations accurately. Additionally, make sure to shade the region of intersection correctly when solving systems with inequalities.