Surface Area of Prism and Pyramids Made Easy
Understanding the Basics of Surface Area
When dealing with three-dimensional shapes, the surface area is a crucial concept to grasp. It refers to the total area covered by the surface of a three-dimensional shape. Calculating the surface area of various shapes, such as prisms and pyramids, can be a challenging task, but with the right approach, it can be made easy.
What is a Prism?
A prism is a three-dimensional shape with two identical faces that are parallel and oriented in the same direction. The other faces of the prism are rectangles, and the number of these rectangular faces depends on the number of sides of the base shape. For example, a triangular prism has three rectangular faces, while a hexagonal prism has six.
What is a Pyramid?
A pyramid is a three-dimensional shape with a base that is a polygon, and the other faces are triangular, meeting at the apex. The number of triangular faces depends on the number of sides of the base shape. For example, a triangular pyramid has three triangular faces, while a square pyramid has four.
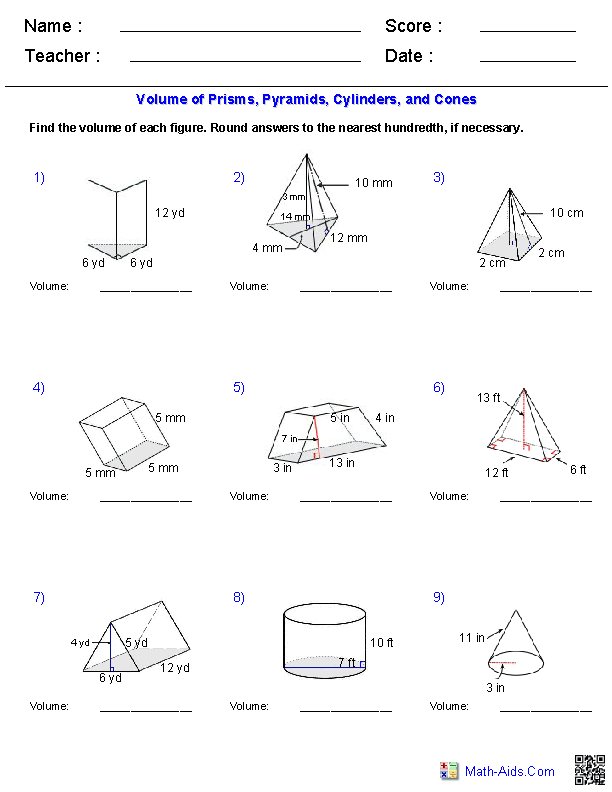
Calculating the Surface Area of a Prism
To calculate the surface area of a prism, you need to calculate the area of the two identical faces and add it to the area of the rectangular faces. The formula for the surface area of a prism is:
Surface Area = 2 × Area of Base + Perimeter of Base × Height
Where:
- Area of Base is the area of one of the identical faces
- Perimeter of Base is the perimeter of the base shape
- Height is the height of the prism
For example, if you have a triangular prism with a base area of 10 square units, a perimeter of 12 units, and a height of 5 units, the surface area would be:
Surface Area = 2 × 10 + 12 × 5 = 20 + 60 = 80 square units
Calculating the Surface Area of a Pyramid
To calculate the surface area of a pyramid, you need to calculate the area of the base and add it to the area of the triangular faces. The formula for the surface area of a pyramid is:
Surface Area = Area of Base + (Number of Triangular Faces × Area of Each Triangular Face)
Where:
- Area of Base is the area of the base shape
- Number of Triangular Faces is the number of triangular faces of the pyramid
- Area of Each Triangular Face is the area of each triangular face
For example, if you have a square pyramid with a base area of 16 square units and four triangular faces, each with an area of 10 square units, the surface area would be:
Surface Area = 16 + (4 × 10) = 16 + 40 = 56 square units
Using the Slant Height to Calculate the Surface Area of a Pyramid
Another way to calculate the surface area of a pyramid is to use the slant height. The slant height is the distance from the apex of the pyramid to the midpoint of one of the sides of the base. The formula for the surface area of a pyramid using the slant height is:
Surface Area = Area of Base + (Number of Triangular Faces × 0.5 × Base Side × Slant Height)
Where:
- Area of Base is the area of the base shape
- Number of Triangular Faces is the number of triangular faces of the pyramid
- Base Side is the length of one side of the base shape
- Slant Height is the slant height of the pyramid
For example, if you have a square pyramid with a base area of 16 square units, four triangular faces, a base side length of 4 units, and a slant height of 6 units, the surface area would be:
Surface Area = 16 + (4 × 0.5 × 4 × 6) = 16 + 48 = 64 square units
Notes
📝 Note: The formulas for the surface area of a prism and pyramid assume that the shapes are right prisms and pyramids, meaning that the base is perpendicular to the height. If the shapes are not right prisms or pyramids, the formulas may need to be adjusted.
📝 Note: The surface area of a prism or pyramid can be used to calculate the volume of the shape, as well as the surface area to volume ratio.
Conclusion
Calculating the surface area of a prism or pyramid can be a complex task, but with the right formulas and approach, it can be made easy. By understanding the basics of surface area and using the formulas provided, you can calculate the surface area of various prisms and pyramids with ease. Whether you are a student or a professional, mastering the concept of surface area is essential for success in mathematics and real-world applications.
What is the difference between a prism and a pyramid?
+
A prism is a three-dimensional shape with two identical faces that are parallel and oriented in the same direction, while a pyramid is a three-dimensional shape with a base that is a polygon, and the other faces are triangular, meeting at the apex.
How do I calculate the surface area of a prism?
+
The surface area of a prism can be calculated using the formula: Surface Area = 2 × Area of Base + Perimeter of Base × Height.
What is the slant height of a pyramid?
+
The slant height of a pyramid is the distance from the apex of the pyramid to the midpoint of one of the sides of the base.
Related Terms:
- Surface area of pyramids worksheet