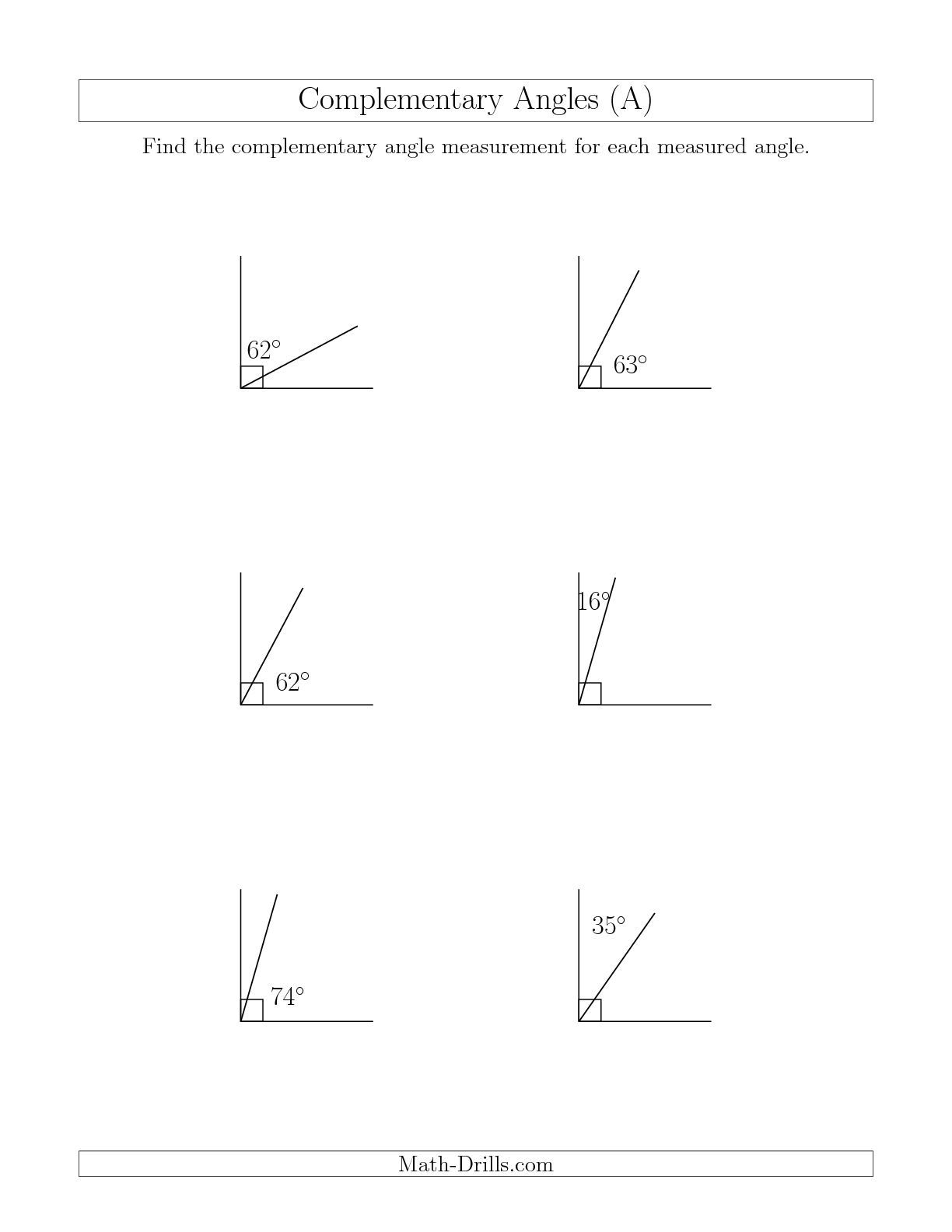
Complementary Angles Worksheet: Find the Missing Angle
Understanding Complementary Angles
Complementary angles are two angles whose measures add up to 90 degrees. These angles are used extensively in geometry and trigonometry to solve various problems involving right triangles and other geometric shapes. Understanding complementary angles is crucial for identifying missing angles in various mathematical problems.
The Concept of Complementary Angles
Complementary angles are defined as two angles whose measures add up to 90 degrees. In other words, if we have two angles, A and B, and their sum is 90 degrees, then they are complementary angles. This concept can be expressed mathematically as:
A + B = 90 degrees
Importance of Complementary Angles
Complementary angles have numerous applications in mathematics, particularly in geometry and trigonometry. They are used to:
- Solve problems involving right triangles
- Find missing angles in geometric shapes
- Calculate trigonometric ratios
- Solve problems involving perpendicular lines and angles
How to Find the Missing Angle
To find the missing angle in a problem involving complementary angles, follow these steps:
- Identify the given angle and its measure.
- Use the formula A + B = 90 degrees to find the measure of the missing angle.
- Substitute the value of the given angle into the formula and solve for the missing angle.
Example Problems
Here are some example problems to illustrate how to find the missing angle using complementary angles:
Problem 1:
Find the missing angle in the following problem:
Angle A = 30 degrees Angle B =?
Solution:
A + B = 90 degrees 30 + B = 90 B = 60 degrees
Therefore, the missing angle is 60 degrees.
Problem 2:
Find the missing angle in the following problem:
Angle A = 45 degrees Angle B =?
Solution:
A + B = 90 degrees 45 + B = 90 B = 45 degrees
Therefore, the missing angle is 45 degrees.
Complementary Angles Worksheet
Here is a worksheet with 10 problems to help you practice finding the missing angle using complementary angles:
| Problem # | Angle A | Angle B |
|---|---|---|
| 1 | 20 degrees | ? |
| 2 | 35 degrees | ? |
| 3 | 50 degrees | ? |
| 4 | 25 degrees | ? |
| 5 | 40 degrees | ? |
| 6 | 55 degrees | ? |
| 7 | 30 degrees | ? |
| 8 | 45 degrees | ? |
| 9 | 20 degrees | ? |
| 10 | 35 degrees | ? |
🤔 Note: Use the formula A + B = 90 degrees to find the missing angle.
Solution to Worksheet
Here are the solutions to the worksheet:
| Problem # | Angle A | Angle B | Solution |
|---|---|---|---|
| 1 | 20 degrees | 70 degrees | 70 degrees |
| 2 | 35 degrees | 55 degrees | 55 degrees |
| 3 | 50 degrees | 40 degrees | 40 degrees |
| 4 | 25 degrees | 65 degrees | 65 degrees |
| 5 | 40 degrees | 50 degrees | 50 degrees |
| 6 | 55 degrees | 35 degrees | 35 degrees |
| 7 | 30 degrees | 60 degrees | 60 degrees |
| 8 | 45 degrees | 45 degrees | 45 degrees |
| 9 | 20 degrees | 70 degrees | 70 degrees |
| 10 | 35 degrees | 55 degrees | 55 degrees |
Conclusion
In this article, we discussed the concept of complementary angles and their importance in mathematics. We also provided a worksheet with 10 problems to help you practice finding the missing angle using complementary angles. By following the steps outlined in this article and practicing with the worksheet, you can improve your understanding of complementary angles and become proficient in finding the missing angle in various mathematical problems.
What are complementary angles?
+Complementary angles are two angles whose measures add up to 90 degrees.
How do I find the missing angle using complementary angles?
+Use the formula A + B = 90 degrees, where A and B are the two angles. Substitute the value of the given angle into the formula and solve for the missing angle.
What is the importance of complementary angles in mathematics?
+Complementary angles are used extensively in geometry and trigonometry to solve problems involving right triangles and other geometric shapes.