Special Segments In Triangles Worksheet
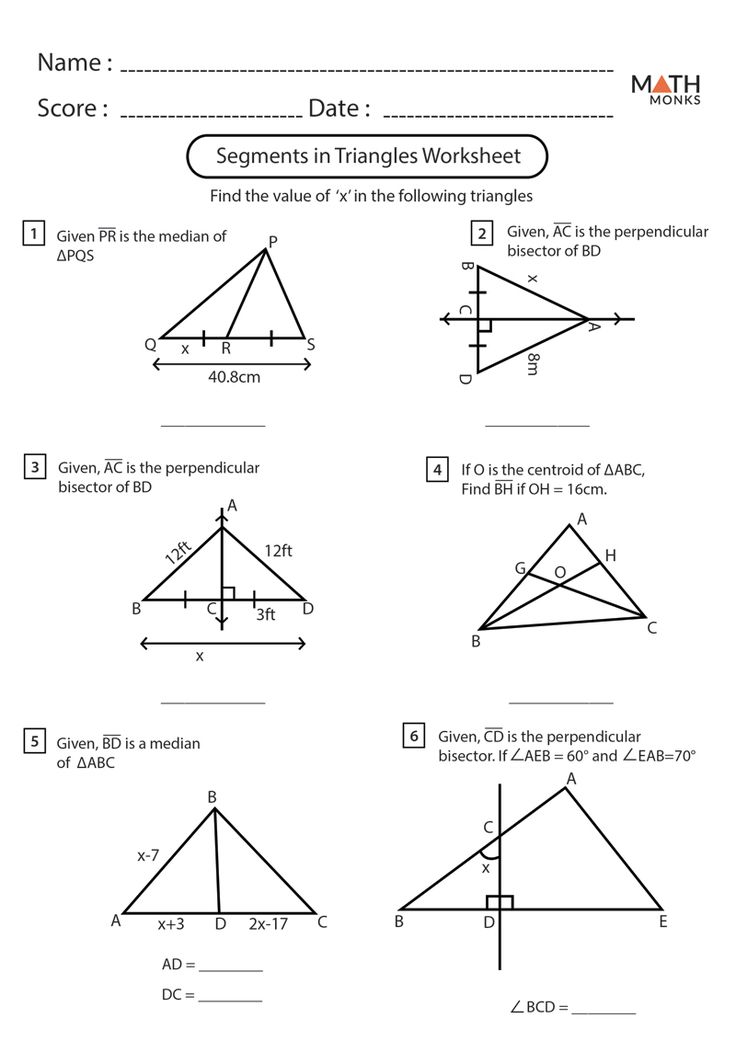
Understanding Special Segments in Triangles
Triangles are one of the most fundamental shapes in geometry, and understanding their properties is crucial for solving various mathematical problems. One of the key concepts in triangle geometry is the special segments that can be found within a triangle. In this article, we will delve into the world of special segments in triangles, exploring their definitions, properties, and applications.
What are Special Segments in Triangles?
Special segments in triangles refer to specific lines or segments that have unique properties and play a crucial role in understanding the geometry of triangles. These segments can be used to solve problems, find missing lengths, and determine the relationships between different parts of the triangle. The three main types of special segments in triangles are:
- Altitudes: An altitude is a line segment that extends from a vertex of a triangle to the opposite side, forming a right angle.
- Medians: A median is a line segment that extends from a vertex of a triangle to the midpoint of the opposite side.
- Angle Bisectors: An angle bisector is a line segment that divides an angle into two equal parts.
Properties of Special Segments
Each type of special segment has unique properties that make them useful for solving problems. Here are some of the key properties of special segments:
- Altitudes:
- An altitude is always perpendicular to the base of the triangle.
- The three altitudes of a triangle intersect at a single point, called the orthocenter.
- Medians:
- A median always divides the opposite side into two equal parts.
- The three medians of a triangle intersect at a single point, called the centroid.
- The centroid divides each median into two segments, one of which is twice as long as the other.
- Angle Bisectors:
- An angle bisector always divides the opposite side into two segments that are proportional to the other two sides.
- The three angle bisectors of a triangle intersect at a single point, called the incenter.
Applications of Special Segments
Special segments have numerous applications in various fields, including:
- Geometry: Special segments are used to solve problems involving triangle congruence, similarity, and right triangles.
- Trigonometry: Special segments are used to find missing lengths and angles in triangles.
- Engineering: Special segments are used in design and construction to ensure that buildings and bridges are stable and secure.
- Physics: Special segments are used to describe the motion of objects and the forces acting upon them.
Worksheet: Special Segments in Triangles
Now that we have explored the world of special segments in triangles, it’s time to practice! Here is a worksheet to help you reinforce your understanding of special segments:
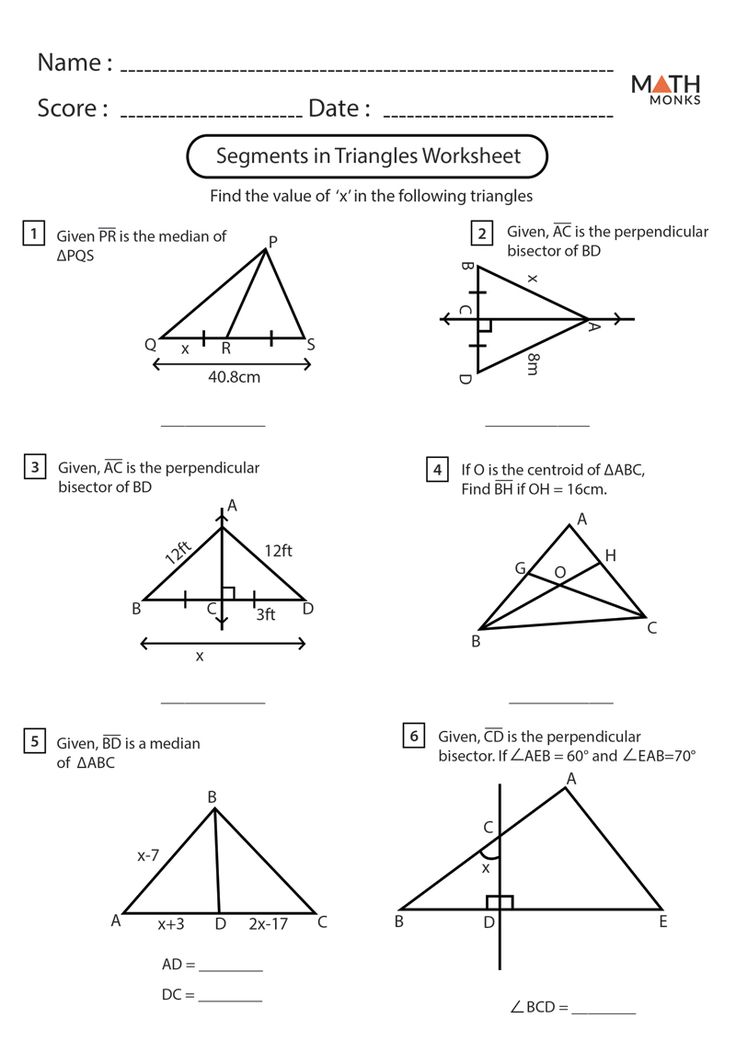
| Problem | Solution |
|---|---|
| 1. In triangle ABC, find the length of the altitude from vertex A to side BC. | Use the Pythagorean theorem to find the length of the altitude. |
| 2. In triangle DEF, find the midpoint of side DE. | Use the midpoint formula to find the midpoint. |
| 3. In triangle GHI, find the length of the angle bisector from vertex G to side HI. | Use the angle bisector theorem to find the length of the angle bisector. |
| 4. In triangle JKL, find the orthocenter of the triangle. | Use the properties of altitudes to find the orthocenter. |
| 5. In triangle MNO, find the centroid of the triangle. | Use the properties of medians to find the centroid. |
📝 Note: Make sure to use the correct formulas and theorems to solve each problem. Show your work and explain your reasoning.
Conclusion
In conclusion, special segments in triangles are a fundamental concept in geometry that has numerous applications in various fields. By understanding the properties and applications of special segments, you can solve a wide range of problems involving triangles. Remember to practice regularly and use the correct formulas and theorems to reinforce your understanding of special segments.
What is the difference between an altitude and an angle bisector?
+An altitude is a line segment that extends from a vertex of a triangle to the opposite side, forming a right angle, whereas an angle bisector is a line segment that divides an angle into two equal parts.
What is the centroid of a triangle?
+The centroid of a triangle is the point of intersection of the three medians. It divides each median into two segments, one of which is twice as long as the other.
How do you find the orthocenter of a triangle?
+The orthocenter of a triangle is the point of intersection of the three altitudes. To find the orthocenter, draw the altitudes of the triangle and find the point where they intersect.