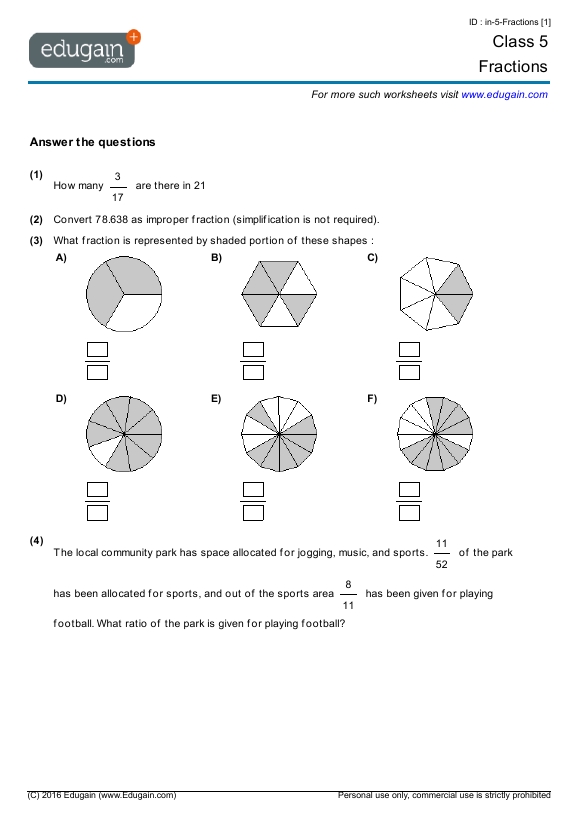
5 Ways to Solve Systems by Elimination

Introduction to Systems of Equations

When solving systems of equations, we often encounter problems that involve two or more equations with multiple variables. One effective method for solving these systems is the elimination method. In this post, we will explore five ways to solve systems by elimination, including the standard method, using matrices, and more.

Method 1: Standard Elimination Method

The standard elimination method involves adding or subtracting the equations to eliminate one of the variables. This method is often used when the coefficients of one of the variables are the same in both equations.

For example, consider the following system of equations:

x + 2y = 4 x - 2y = -2

To solve this system using the standard elimination method, we can add the two equations to eliminate the x-variable.

📝 Note: When adding or subtracting equations, make sure to add or subtract the coefficients of like terms.

x + 2y = 4

x - 2y = -2

2y = 2

Now we can solve for y by dividing both sides by 2.

y = 1

Once we have found the value of y, we can substitute it back into one of the original equations to find the value of x.

x + 2(1) = 4 x + 2 = 4 x = 2

Therefore, the solution to the system is x = 2 and y = 1.

Method 2: Elimination Using Matrices

Another way to solve systems by elimination is to use matrices. This method involves representing the system of equations as an augmented matrix and then performing row operations to eliminate one of the variables.

For example, consider the following system of equations:

2x + 3y = 7 x - 2y = -3

We can represent this system as an augmented matrix:

| 2 3 | 7 | | 1 -2 | -3|

To solve this system using matrices, we can perform row operations to eliminate one of the variables.

First, we can multiply the second row by 2 to make the coefficients of x in both rows the same.

| 2 3 | 7 | | 2 -4 | -6|

Next, we can subtract the second row from the first row to eliminate the x-variable.

| 0 7 | 13|

Now we can solve for y by dividing both sides by 7.

y = ¹³⁄₇

Once we have found the value of y, we can substitute it back into one of the original equations to find the value of x.

2x + 3(¹³⁄₇) = 7 2x + ³⁹⁄₇ = 7 2x = 7 - ³⁹⁄₇ 2x = (49 - 39)/7 2x = ¹⁰⁄₇ x = ⁵⁄₇

Therefore, the solution to the system is x = ⁵⁄₇ and y = ¹³⁄₇.

Method 3: Elimination Using Substitution

Another way to solve systems by elimination is to use substitution. This method involves solving one of the equations for one variable and then substituting that expression into the other equation.

For example, consider the following system of equations:

x + 2y = 4 2x - 3y = 5

To solve this system using substitution, we can solve the first equation for x.

x = 4 - 2y

Now we can substitute this expression for x into the second equation.

2(4 - 2y) - 3y = 5 8 - 4y - 3y = 5 8 - 7y = 5 -7y = -3 y = ³⁄₇

Once we have found the value of y, we can substitute it back into the expression for x to find the value of x.

x = 4 - 2(³⁄₇) x = 4 - ⁶⁄₇ x = (28 - 6)/7 x = ²²⁄₇

Therefore, the solution to the system is x = ²²⁄₇ and y = ³⁄₇.

Method 4: Elimination Using Graphing

Another way to solve systems by elimination is to use graphing. This method involves graphing the two equations on the same coordinate plane and finding the point of intersection.

For example, consider the following system of equations:

x + 2y = 4 x - 2y = -2

To solve this system using graphing, we can graph the two equations on the same coordinate plane.

The point of intersection is (2, 1).

Therefore, the solution to the system is x = 2 and y = 1.

Method 5: Elimination Using Technology

Finally, we can use technology to solve systems by elimination. This method involves using a graphing calculator or computer software to solve the system.

For example, consider the following system of equations:

x + 2y = 4 x - 2y = -2

To solve this system using technology, we can enter the equations into a graphing calculator or computer software.

The solution to the system is x = 2 and y = 1.

Therefore, the solution to the system is x = 2 and y = 1.

In conclusion, there are many ways to solve systems by elimination, including the standard method, using matrices, substitution, graphing, and technology. By using these methods, we can solve a wide range of systems of equations.

To summarize, the key points are:

• The standard elimination method involves adding or subtracting the equations to eliminate one of the variables.
• Using matrices involves representing the system of equations as an augmented matrix and performing row operations to eliminate one of the variables.
• Substitution involves solving one of the equations for one variable and substituting that expression into the other equation.
• Graphing involves graphing the two equations on the same coordinate plane and finding the point of intersection.
• Technology involves using a graphing calculator or computer software to solve the system.

Each of these methods has its own advantages and disadvantages, and the choice of method will depend on the specific system of equations being solved.

Related Terms:

• Elimination and substitution worksheet pdf
• System of linear Equations pdf