5 Ways to Master Fractions with Worksheets
Mastering Fractions: A Comprehensive Guide with Worksheets
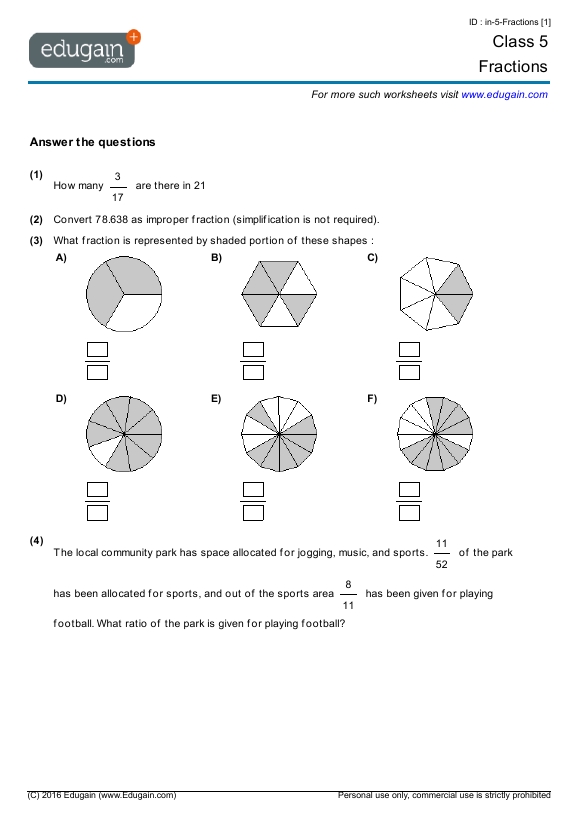
Fractions are a fundamental concept in mathematics, and mastering them is crucial for success in various mathematical operations. However, fractions can be a challenging topic for many students, especially when it comes to adding, subtracting, multiplying, and dividing them. In this article, we will provide you with 5 effective ways to master fractions, along with worksheets to help you practice and reinforce your understanding.
1. Understanding the Basics of Fractions
Before diving into complex fraction operations, it’s essential to understand the basics. A fraction represents a part of a whole, and it consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 3⁄4, the numerator is 3, and the denominator is 4.
To master fractions, you need to understand the following concepts:
- Equivalent fractions: Fractions that have the same value, but different numerators and denominators. For example, 1⁄2 = 2⁄4 = 3⁄6.
- Simplifying fractions: Reducing a fraction to its simplest form by dividing both the numerator and denominator by the greatest common divisor (GCD). For example, 6⁄8 = 3⁄4.
- Comparing fractions: Determining which fraction is greater or lesser than another. For example, 1⁄2 > 1⁄3.
Worksheets:
| Fraction | Equivalent Fraction | Simplified Fraction |
|---|---|---|
| 2⁄4 | 1⁄2 | 1⁄2 |
| 3⁄6 | 1⁄2 | 1⁄2 |
| 4⁄8 | 1⁄2 | 1⁄2 |
2. Adding and Subtracting Fractions
Adding and subtracting fractions is a crucial concept in mathematics. To add or subtract fractions, you need to follow these steps:
- Find a common denominator: The least common multiple (LCM) of the denominators.
- Convert fractions to have the common denominator: Multiply the numerator and denominator by the necessary multiples.
- Add or subtract the fractions: Add or subtract the numerators, keeping the common denominator the same.
For example:
2⁄4 + 1⁄6 =?
- Find a common denominator: LCM(4, 6) = 12
- Convert fractions to have the common denominator: 2⁄4 = 6⁄12, 1⁄6 = 2⁄12
- Add the fractions: 6⁄12 + 2⁄12 = 8⁄12
Worksheets:
| Fraction 1 | Fraction 2 | Sum/Difference |
|---|---|---|
| 1⁄2 | 1⁄4 | 3⁄4 |
| 2⁄3 | 1⁄6 | 5⁄6 |
| 3⁄4 | 2⁄8 | 5⁄8 |
3. Multiplying Fractions
Multiplying fractions is a straightforward process. To multiply fractions, you simply multiply the numerators and denominators:
- Multiply the numerators: Multiply the top numbers.
- Multiply the denominators: Multiply the bottom numbers.
For example:
1⁄2 × 3⁄4 =?
- Multiply the numerators: 1 × 3 = 3
- Multiply the denominators: 2 × 4 = 8
- Multiply the fractions: 3⁄8
Worksheets:
| Fraction 1 | Fraction 2 | Product |
|---|---|---|
| 1⁄2 | 2⁄3 | 2⁄6 |
| 3⁄4 | 1⁄2 | 3⁄8 |
| 2⁄5 | 3⁄4 | 6⁄20 |
4. Dividing Fractions
Dividing fractions is equivalent to multiplying by the reciprocal of the divisor. To divide fractions, you need to follow these steps:
- Invert the divisor: Flip the numerator and denominator of the divisor.
- Multiply the fractions: Multiply the numerators and denominators.
For example:
1⁄2 ÷ 3⁄4 =?
- Invert the divisor: 3⁄4 → 4⁄3
- Multiply the fractions: 1⁄2 × 4⁄3 = 4⁄6
Worksheets:
| Fraction 1 | Fraction 2 | Quotient |
|---|---|---|
| 1⁄2 | 3⁄4 | 2⁄3 |
| 2⁄3 | 1⁄2 | 4⁄3 |
| 3⁄4 | 2⁄5 | 15⁄8 |
5. Real-World Applications of Fractions
Fractions have numerous real-world applications, such as:
- Cooking: Measuring ingredients using fractions.
- Shopping: Comparing prices and discounts using fractions.
- Science: Measuring quantities using fractions.
Worksheets:
| Scenario | Fraction | Solution |
|---|---|---|
| Recipe calls for 3⁄4 cup of sugar | 1⁄2 cup sugar available | Add 1⁄4 cup sugar |
| Discount of 1⁄2 on a shirt | Original price $20 | Pay $10 |
| Laboratory measurement: 2⁄3 liter | Convert to milliliters | 667 milliliters |
Notes:
- When simplifying fractions, always divide both the numerator and denominator by the GCD.
- When comparing fractions, always convert to equivalent fractions with the same denominator.
What is the definition of a fraction?
+A fraction represents a part of a whole, and it consists of a numerator (the top number) and a denominator (the bottom number).
How do I add and subtract fractions?
+To add or subtract fractions, find a common denominator, convert fractions to have the common denominator, and then add or subtract the numerators.
What is the difference between multiplying and dividing fractions?
+Multiplying fractions involves multiplying the numerators and denominators, while dividing fractions involves inverting the divisor and multiplying.
In conclusion, mastering fractions requires practice and a deep understanding of the underlying concepts. By following these 5 effective ways to master fractions, along with the provided worksheets, you’ll be well on your way to becoming a fraction expert.