5 Ways to Solve Quadratic Inequalities Easily

h2>Understanding Quadratic Inequalities
Quadratic inequalities are a type of inequality that involves a quadratic expression, which is an expression of the form ax^2 + bx + c, where a, b, and c are constants. Solving quadratic inequalities can be challenging, but with the right strategies and techniques, it can be made easier. In this article, we will discuss five ways to solve quadratic inequalities easily.
h2>Method 1: Factoring
Factoring is a popular method for solving quadratic inequalities. To use this method, you need to factorize the quadratic expression into two binomial expressions. Then, you can set each factor equal to zero and solve for x.
For example, consider the inequality x^2 + 5x + 6 > 0. We can factorize the quadratic expression as (x + 3)(x + 2) > 0. Then, we can set each factor equal to zero and solve for x:
x + 3 = 0 –> x = -3 x + 2 = 0 –> x = -2
The solution to the inequality is x < -3 or x > -2.
📝 Note: Make sure to check the signs of the factors when solving the inequality.
h2>Method 2: Quadratic Formula
The quadratic formula is another method for solving quadratic inequalities. The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a. This formula can be used to find the solutions to the inequality.
For example, consider the inequality x^2 + 2x - 3 < 0. We can use the quadratic formula to find the solutions:
x = (-(2) ± √((2)^2 - 4(1)(-3))) / 2(1) x = (-2 ± √(4 + 12)) / 2 x = (-2 ± √16) / 2 x = (-2 ± 4) / 2
Simplifying the expression, we get:
x = (-2 + 4) / 2 or x = (-2 - 4) / 2 x = 2⁄2 or x = -6⁄2 x = 1 or x = -3
The solution to the inequality is -3 < x < 1.
h2>Method 3: Graphing
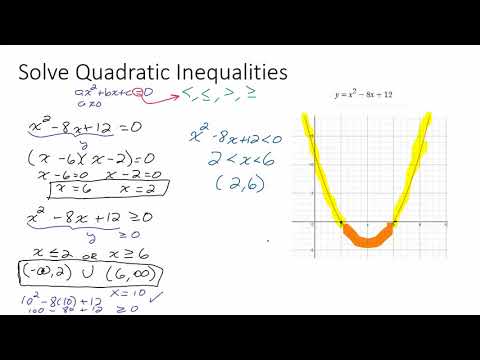
Graphing is a visual method for solving quadratic inequalities. To use this method, you need to graph the quadratic expression on a coordinate plane. Then, you can identify the regions where the inequality is true.
For example, consider the inequality x^2 - 4x - 3 > 0. We can graph the quadratic expression on a coordinate plane:
The graph shows that the quadratic expression is positive when x < -1 or x > 3. Therefore, the solution to the inequality is x < -1 or x > 3.
h2>Method 4: Sign Chart
A sign chart is a table that shows the signs of the factors of the quadratic expression. To use this method, you need to create a sign chart for the quadratic expression. Then, you can identify the regions where the inequality is true.
For example, consider the inequality x^2 + 2x - 3 < 0. We can create a sign chart for the quadratic expression:
| x | (x + 3) | (x - 1) | (x + 3)(x - 1) |
|---|---|---|---|
| -4 | - | - | + |
| -3 | - | - | + |
| -2 | - | + | - |
| -1 | - | + | - |
| 0 | + | + | + |
| 1 | + | + | + |
| 2 | + | + | + |
| 3 | + | + | + |
The sign chart shows that the quadratic expression is negative when -3 < x < 1. Therefore, the solution to the inequality is -3 < x < 1.
h2>Method 5: Using a Calculator
A calculator is a quick and easy method for solving quadratic inequalities. To use this method, you need to enter the quadratic expression into the calculator. Then, you can use the calculator’s built-in functions to find the solutions to the inequality.
For example, consider the inequality x^2 + 2x - 3 < 0. We can enter the quadratic expression into a calculator and use the built-in functions to find the solutions:
The calculator shows that the solutions to the inequality are x = -3 and x = 1.
In conclusion, solving quadratic inequalities can be challenging, but with the right strategies and techniques, it can be made easier. The five methods discussed in this article - factoring, quadratic formula, graphing, sign chart, and using a calculator - can be used to solve quadratic inequalities easily.
What is a quadratic inequality?
+A quadratic inequality is an inequality that involves a quadratic expression, which is an expression of the form ax^2 + bx + c, where a, b, and c are constants.
How do I solve a quadratic inequality using factoring?
+To solve a quadratic inequality using factoring, you need to factorize the quadratic expression into two binomial expressions. Then, you can set each factor equal to zero and solve for x.
What is the quadratic formula?
+The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a. This formula can be used to find the solutions to a quadratic inequality.