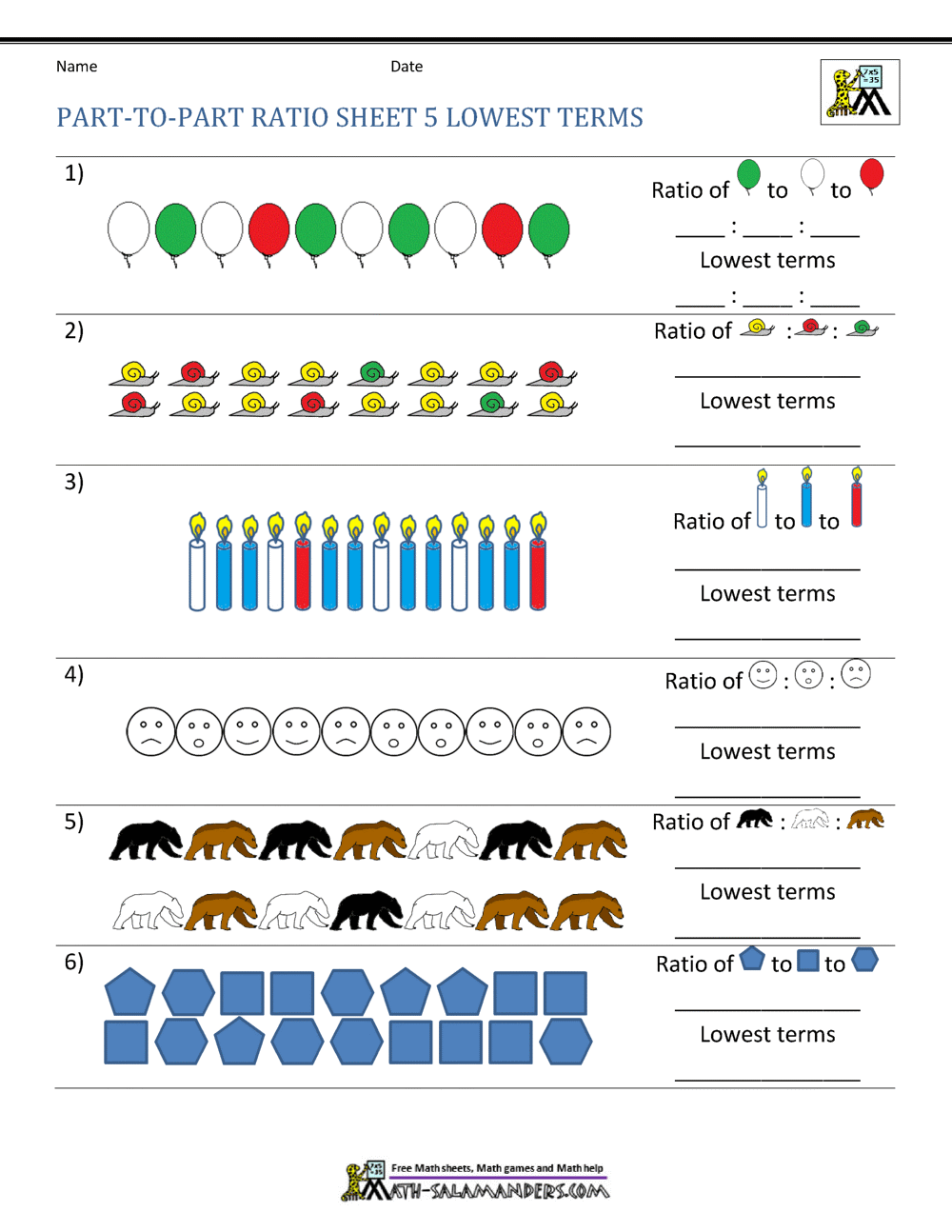
5 Essential Rules for Exponents
Understanding Exponents: A Comprehensive Guide
Exponents are a fundamental concept in mathematics, and understanding their rules is crucial for simplifying expressions and solving equations. In this blog post, we will delve into the world of exponents, exploring the five essential rules that govern their behavior. Whether you’re a student, teacher, or simply a math enthusiast, this guide will provide you with a solid foundation in exponent rules, enabling you to tackle complex math problems with confidence.
Rule 1: The Product Rule
The product rule states that when multiplying two numbers with the same base, you can add their exponents. Mathematically, this can be represented as:
am × an = am+n
For example, let’s consider the expression 23 × 24. Using the product rule, we can simplify this to:
23+4 = 27
📝 Note: This rule only applies when the bases are the same. If the bases are different, you cannot simplify the expression using the product rule.
Rule 2: The Quotient Rule
The quotient rule is the opposite of the product rule. When dividing two numbers with the same base, you subtract their exponents. Mathematically, this can be represented as:
am ÷ an = am-n
For example, let’s consider the expression 27 ÷ 23. Using the quotient rule, we can simplify this to:
27-3 = 24
📝 Note: Like the product rule, the quotient rule only applies when the bases are the same.
Rule 3: The Power Rule
The power rule states that when raising a power to another power, you multiply the exponents. Mathematically, this can be represented as:
(am)n = am×n
For example, let’s consider the expression (23)4. Using the power rule, we can simplify this to:
23×4 = 212
Rule 4: The Zero Rule
The zero rule states that any number raised to the power of zero is equal to 1. Mathematically, this can be represented as:
a0 = 1
For example, let’s consider the expression 20. Using the zero rule, we can simplify this to:
20 = 1
Rule 5: The Negative Rule
The negative rule states that when a number is raised to a negative power, you can rewrite it as the reciprocal of the base raised to the positive power. Mathematically, this can be represented as:
a-m = 1/am
For example, let’s consider the expression 2-3. Using the negative rule, we can rewrite this as:
2-3 = 1⁄23
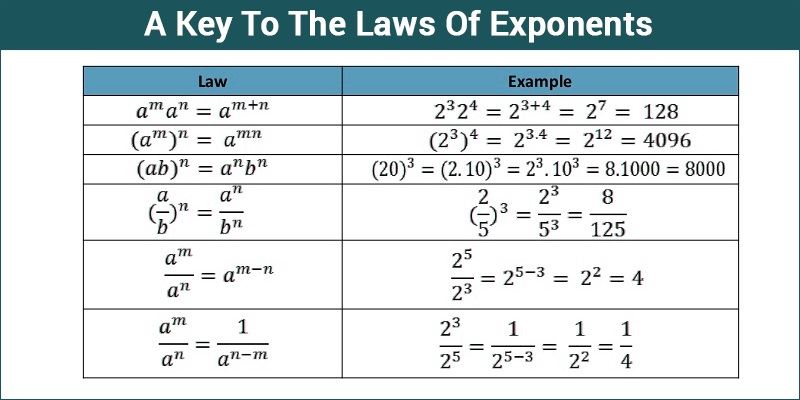
| Rule | Mathematical Representation | Example |
|---|---|---|
| Product Rule | am × an = am+n | 23 × 24 = 27 |
| Quotient Rule | am ÷ an = am-n | 27 ÷ 23 = 24 |
| Power Rule | (am)n = am×n | (23)4 = 212 |
| Zero Rule | a0 = 1 | 20 = 1 |
| Negative Rule | a-m = 1/am | 2-3 = 1/23 |
To recap, we’ve explored the five essential rules for exponents: the product rule, quotient rule, power rule, zero rule, and negative rule. Understanding these rules is crucial for simplifying expressions and solving equations. By applying these rules, you’ll be able to tackle complex math problems with confidence.
What is the product rule for exponents?
+The product rule states that when multiplying two numbers with the same base, you can add their exponents. Mathematically, this can be represented as: am × an = am+n
What is the quotient rule for exponents?
+The quotient rule states that when dividing two numbers with the same base, you subtract their exponents. Mathematically, this can be represented as: am ÷ an = am-n
What is the power rule for exponents?
+The power rule states that when raising a power to another power, you multiply the exponents. Mathematically, this can be represented as: (am)n = am×n
Related Terms:
- Exponent exercises pdf
- Exponent Worksheet
- Exponents worksheets PDF with answers
- Exponent pdf