5 Ways to Master Parallel Lines with Transversal
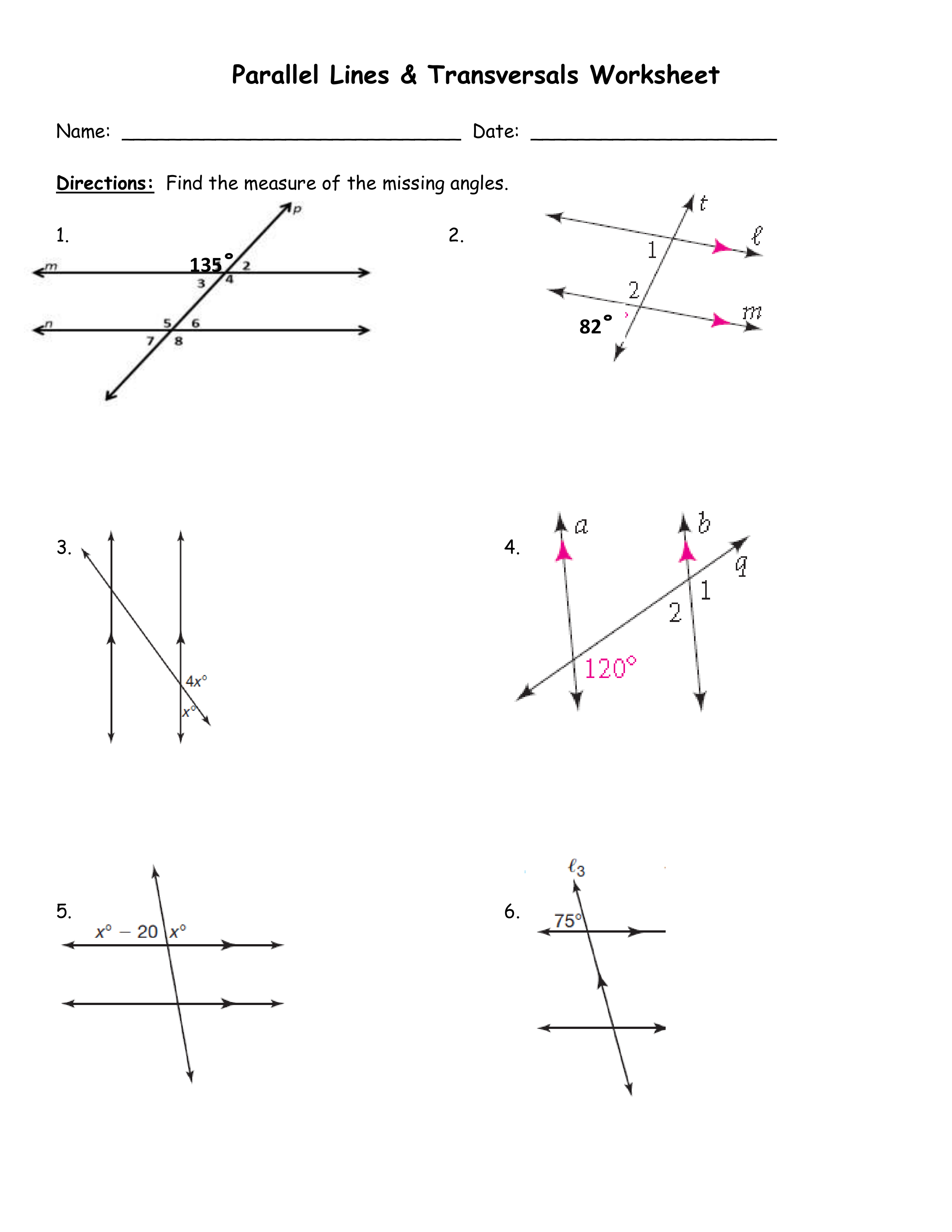
Understanding Parallel Lines and Transversals
Parallel lines are two or more lines that lie in the same plane and never intersect, no matter how far they are extended. A transversal, on the other hand, is a line that intersects two or more other lines. When a transversal intersects two parallel lines, it forms pairs of angles that have specific relationships. Mastering these relationships is crucial for solving problems involving parallel lines and transversals.
1. Identifying Corresponding Angles
When a transversal intersects two parallel lines, it forms pairs of corresponding angles. Corresponding angles are angles that are in the same relative position in each of the intersected lines. These angles are always congruent, meaning they have the same measure.

For example, in the diagram above, ∠A and ∠E are corresponding angles, as are ∠B and ∠F. If we know the measure of one of these angles, we can determine the measure of its corresponding angle.
📝 Note: Corresponding angles are always congruent, but congruent angles are not always corresponding angles.
2. Understanding Alternate Interior Angles
Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines. When a transversal intersects two parallel lines, alternate interior angles are always congruent.

In the diagram above, ∠C and ∠G are alternate interior angles, as are ∠D and ∠H. If we know the measure of one of these angles, we can determine the measure of its alternate interior angle.
3. Working with Alternate Exterior Angles
Alternate exterior angles are angles that are on opposite sides of the transversal and outside the parallel lines. When a transversal intersects two parallel lines, alternate exterior angles are always congruent.

In the diagram above, ∠I and ∠K are alternate exterior angles, as are ∠J and ∠L. If we know the measure of one of these angles, we can determine the measure of its alternate exterior angle.
4. Using Interior Angles on the Same Side of the Transversal
When a transversal intersects two parallel lines, the interior angles on the same side of the transversal are supplementary, meaning they add up to 180 degrees.

In the diagram above, ∠M and ∠N are interior angles on the same side of the transversal. We can use this relationship to find the measure of one angle if we know the measure of the other angle.
5. Applying the Relationships to Real-World Problems
Understanding the relationships between angles formed by a transversal intersecting two parallel lines is crucial for solving problems in various fields, such as architecture, engineering, and design.
| Problem | Solution |
|---|---|
| In a bridge design, two parallel beams are intersected by a support beam. If the angle between the support beam and one of the parallel beams is 60 degrees, what is the angle between the support beam and the other parallel beam? | Since the angles are corresponding angles, they are congruent. Therefore, the angle between the support beam and the other parallel beam is also 60 degrees. |
| In a building design, two parallel walls are intersected by a doorway. If the angle between the doorway and one of the parallel walls is 45 degrees, what is the angle between the doorway and the other parallel wall? | Since the angles are alternate interior angles, they are congruent. Therefore, the angle between the doorway and the other parallel wall is also 45 degrees. |
In conclusion, mastering the relationships between angles formed by a transversal intersecting two parallel lines is essential for solving problems in various fields. By understanding corresponding angles, alternate interior angles, alternate exterior angles, and interior angles on the same side of the transversal, you can apply these relationships to real-world problems and achieve accurate results.
What is the difference between corresponding angles and alternate interior angles?
+Corresponding angles are angles that are in the same relative position in each of the intersected lines, while alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines.
Can corresponding angles be supplementary?
+No, corresponding angles are always congruent, but not necessarily supplementary.
How can I use alternate exterior angles to solve problems?
+Alternate exterior angles can be used to solve problems involving the intersection of two parallel lines and a transversal. If you know the measure of one angle, you can determine the measure of its alternate exterior angle.
Related Terms:
- teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo



