Find Slope Easily with 5 Simple Steps

Understanding Slope and Its Importance in Math
Slope is a fundamental concept in mathematics, particularly in geometry and algebra. It represents the rate of change or steepness of a line. Understanding slope is crucial for solving various mathematical problems, graphing lines, and analyzing functions. In this blog post, we will guide you through 5 simple steps to find slope easily.
What is Slope?
Slope is a measure of how steep a line is. It is calculated by dividing the vertical change (rise) by the horizontal change (run) between two points on the line. Slope can be positive, negative, or zero, indicating the direction and steepness of the line.
Step 1: Identify the Two Points
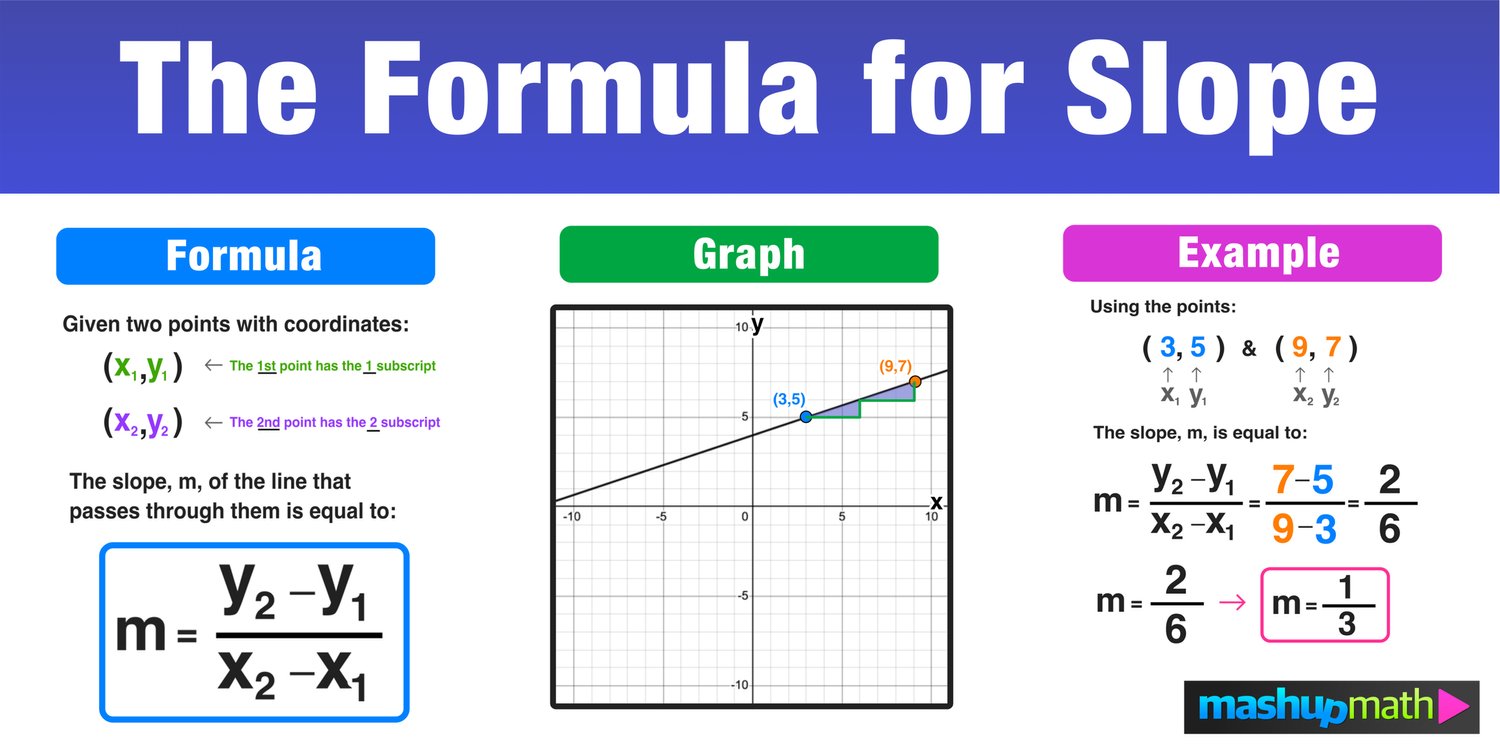
To find the slope of a line, you need to identify two points on the line. These points can be given in the form of coordinates (x, y). Let’s call the two points (x1, y1) and (x2, y2).
📝 Note: Make sure the points are on the line and not on a curve or any other shape.
Step 2: Calculate the Rise (Vertical Change)
The rise is the vertical distance between the two points. It is calculated by subtracting the y-coordinate of the first point (y1) from the y-coordinate of the second point (y2). This will give you the vertical change or rise.
Formula: Rise = y2 - y1
Step 3: Calculate the Run (Horizontal Change)
The run is the horizontal distance between the two points. It is calculated by subtracting the x-coordinate of the first point (x1) from the x-coordinate of the second point (x2). This will give you the horizontal change or run.
Formula: Run = x2 - x1
Step 4: Calculate the Slope
Now that you have the rise and run, you can calculate the slope using the formula:
Slope = Rise / Run
Formula: Slope = (y2 - y1) / (x2 - x1)
📝 Note: Make sure to keep the order of the points consistent. If you swap the points, the slope will be the negative reciprocal of the original slope.
Step 5: Simplify the Slope (Optional)
If the slope is a fraction, you may want to simplify it to its simplest form. This can be done by dividing both the numerator and denominator by their greatest common divisor (GCD).
| Slope | Simplified Slope |
|---|---|
| 3/4 | 3/4 (no simplification needed) |
| 6/8 | 3/4 (simplified) |
By following these 5 simple steps, you can easily find the slope of a line. Remember to identify the two points, calculate the rise and run, and then use the slope formula to get the answer.
What is the difference between slope and steepness?
+Slope and steepness are often used interchangeably, but slope refers to the rate of change or the ratio of vertical to horizontal change, while steepness refers to the general rate of ascent or descent of a line.
Can the slope be zero?
+Yes, the slope can be zero. A slope of zero indicates a horizontal line, which has no vertical change.
Can the slope be negative?
+Yes, the slope can be negative. A negative slope indicates a line that slopes downward from left to right.