5 Ways to Solve Inequalities Easily
Understanding Inequalities and Their Importance in Mathematics
Inequalities are a fundamental concept in mathematics, and solving them is a crucial skill for students to master. Inequalities are statements that compare two expressions using greater than (>), less than (<), greater than or equal to (≥), or less than or equal to (≤) symbols. They are used to solve problems in various mathematical disciplines, including algebra, geometry, and calculus.
In this article, we will explore five ways to solve inequalities easily, along with examples and explanations to help you understand the concepts better.
Method 1: Addition and Subtraction Property
One of the simplest ways to solve inequalities is by using the addition and subtraction property. This property states that if we add or subtract the same value from both sides of an inequality, the inequality remains true.
For example, consider the inequality 2x + 3 > 5. To solve this inequality, we can subtract 3 from both sides:
2x + 3 - 3 > 5 - 3
This simplifies to:
2x > 2
Next, we can divide both sides by 2 to get:
x > 1
Therefore, the solution to the inequality is x > 1.
📝 Note: When using the addition and subtraction property, make sure to perform the same operation on both sides of the inequality to maintain the equality.
Method 2: Multiplication and Division Property
Another way to solve inequalities is by using the multiplication and division property. This property states that if we multiply or divide both sides of an inequality by a positive value, the inequality remains true. However, if we multiply or divide both sides by a negative value, the inequality is reversed.
For example, consider the inequality 4x < 12. To solve this inequality, we can divide both sides by 4:
(4x)/4 < 12⁄4
This simplifies to:
x < 3
Therefore, the solution to the inequality is x < 3.
📝 Note: When using the multiplication and division property, be careful when dividing or multiplying by a negative value, as it can change the direction of the inequality.
Method 3: Isolation of Variables
Isolating variables is another method for solving inequalities. This involves using algebraic operations to isolate the variable on one side of the inequality.
For example, consider the inequality 2x - 5 > 3. To solve this inequality, we can add 5 to both sides:
2x - 5 + 5 > 3 + 5
This simplifies to:
2x > 8
Next, we can divide both sides by 2 to get:
x > 4
Therefore, the solution to the inequality is x > 4.
Method 4: Factoring and Quadratic Inequalities
Factoring and quadratic inequalities are more complex inequalities that require a different approach. To solve these inequalities, we can use factoring or the quadratic formula to isolate the variable.
For example, consider the inequality x^2 + 5x + 6 > 0. To solve this inequality, we can factor the quadratic expression:
(x + 2)(x + 3) > 0
This inequality is true when both factors are positive or both factors are negative. Therefore, the solution to the inequality is x < -3 or x > -2.
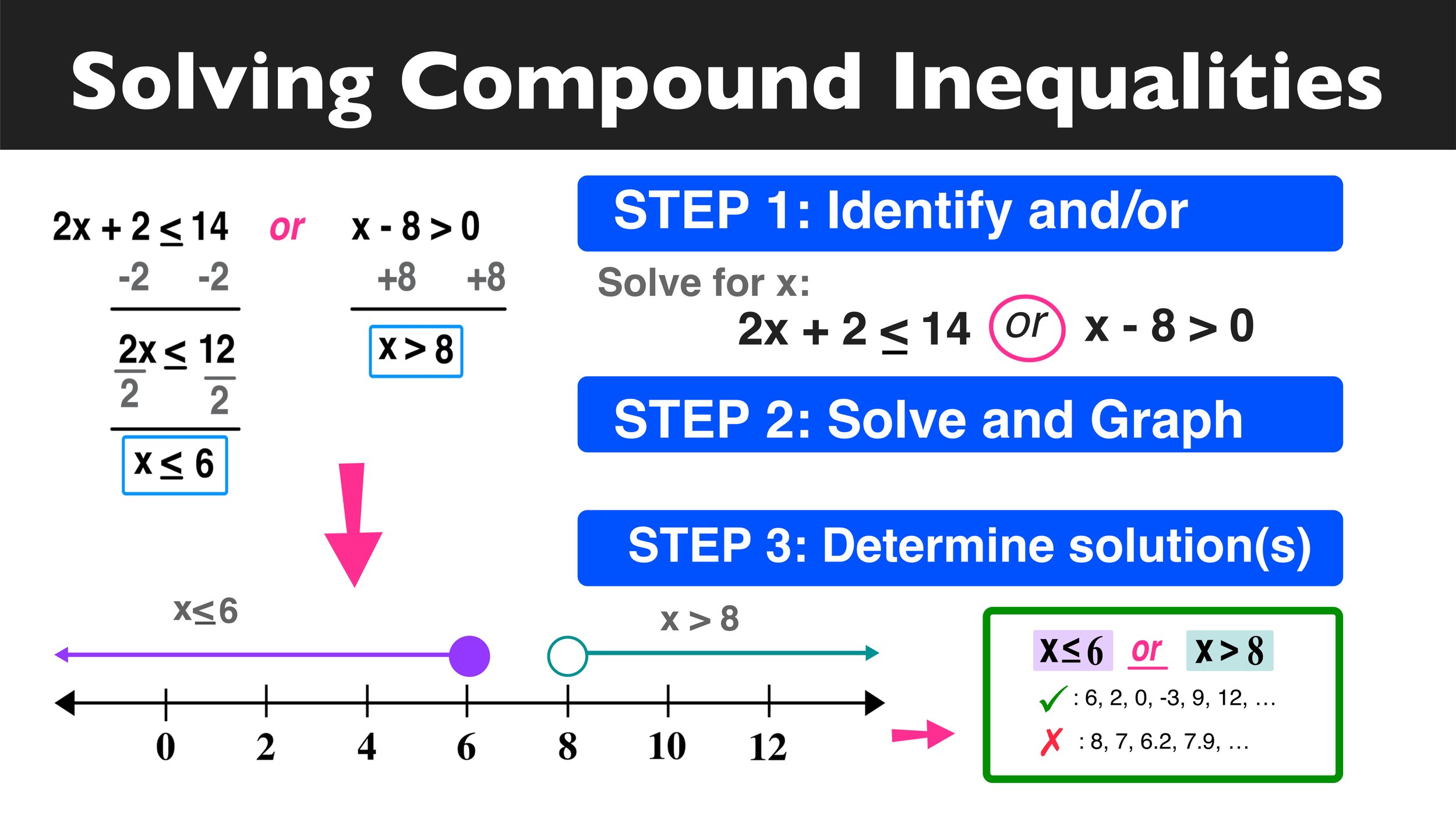
Method 5: Graphing and Interval Notation
Finally, graphing and interval notation can be used to solve inequalities. This involves graphing the inequality on a number line and using interval notation to represent the solution.
For example, consider the inequality x > 2. To solve this inequality, we can graph it on a number line:
Graph: (2, ∞)
The graph shows that the inequality is true for all values of x greater than 2. Therefore, the solution to the inequality is x > 2, which can also be represented in interval notation as (2, ∞).

| Method | Description | Example |
|---|---|---|
| Addition and Subtraction Property | Adding or subtracting the same value from both sides of an inequality | 2x + 3 > 5 ⇒ 2x > 2 |
| Multiplication and Division Property | Multiplying or dividing both sides of an inequality by a positive or negative value | 4x < 12 ⇒ x < 3 |
| Isolation of Variables | Using algebraic operations to isolate the variable on one side of the inequality | 2x - 5 > 3 ⇒ x > 4 |
| Factoring and Quadratic Inequalities | Using factoring or the quadratic formula to isolate the variable in quadratic inequalities | x^2 + 5x + 6 > 0 ⇒ x < -3 or x > -2 |
| Graphing and Interval Notation | Graphing the inequality on a number line and using interval notation to represent the solution | x > 2 ⇒ (2, ∞) |
Solving inequalities is a fundamental skill in mathematics, and there are several methods to solve them. By understanding and applying these methods, you can easily solve inequalities and become proficient in mathematics.
In conclusion, solving inequalities requires a combination of algebraic operations, graphing, and interval notation. By mastering these methods, you can solve a wide range of inequalities and become proficient in mathematics. Remember to always check your solutions and use the correct notation to represent your answers.
What is the difference between an equation and an inequality?
+An equation is a statement that expresses the equality of two mathematical expressions, whereas an inequality is a statement that compares two expressions using greater than, less than, greater than or equal to, or less than or equal to symbols.
How do I know which method to use when solving an inequality?
+The method to use when solving an inequality depends on the type of inequality and the operations involved. You can use the addition and subtraction property, multiplication and division property, isolation of variables, factoring and quadratic inequalities, or graphing and interval notation, depending on the specific inequality.
What is the importance of solving inequalities in mathematics?
+Solving inequalities is crucial in mathematics as it helps to solve problems in various mathematical disciplines, including algebra, geometry, and calculus. Inequalities are used to model real-world problems, and solving them provides a way to analyze and understand complex systems and phenomena.
Related Terms:
- Linear Inequalities worksheet
- Systems of linear inequalities worksheet
- Complex number Worksheet pdf
- Linear graph Worksheet pdf



