5 Ways to Simplify Radicals Made Easy
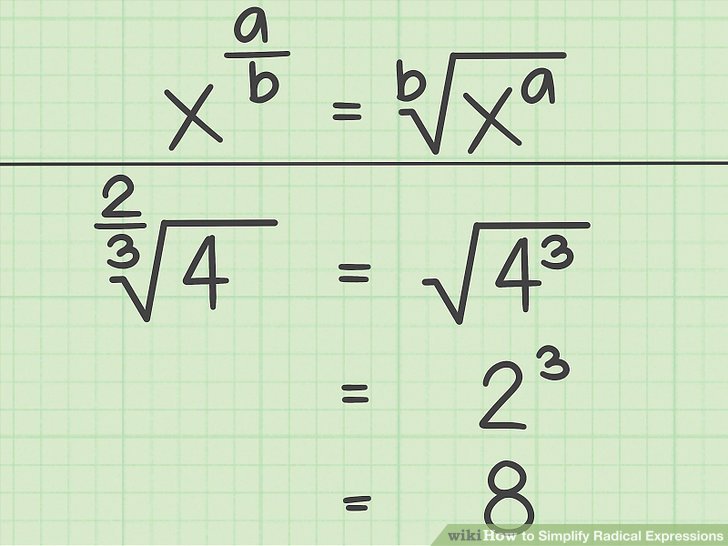
Unlocking the Power of Radicals: Simplification Made Easy
Radicals, or roots, are a fundamental concept in mathematics, and simplifying them is a crucial skill to master. However, many students find radicals intimidating, leading to frustration and confusion. In this article, we’ll break down the process of simplifying radicals into manageable chunks, making it easier for you to grasp and apply these concepts.
Understanding Radicals
Before diving into simplification, it’s essential to understand what radicals represent. A radical is a symbol used to represent the nth root of a number. For example, the square root of 16 is written as √16, and the cube root of 27 is written as ∛27. Radicals can be simplified, and this process involves finding the largest perfect power that can be factored out of the radicand (the number inside the radical).
Method 1: Factoring Out Perfect Squares
One of the simplest ways to simplify radicals is to factor out perfect squares. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. For example, 16 is a perfect square because it can be expressed as 4 × 4.
| Radical | Simplified Form |
|---|---|
| √16 | 4 |
| √24 | 2√6 |
To simplify a radical using this method:
- Identify the perfect square factor of the radicand.
- Write the radical as a product of the perfect square factor and the remaining factor.
- Simplify the perfect square factor by taking its square root.
🤔 Note: This method only works when the radicand has a perfect square factor.
Method 2: Factoring Out Perfect Cubes
Similar to factoring out perfect squares, you can also simplify radicals by factoring out perfect cubes. A perfect cube is a number that can be expressed as the product of an integer multiplied by itself twice. For example, 27 is a perfect cube because it can be expressed as 3 × 3 × 3.
| Radical | Simplified Form |
|---|---|
| ∛27 | 3 |
| ∛48 | 2∛3 |
To simplify a radical using this method:
- Identify the perfect cube factor of the radicand.
- Write the radical as a product of the perfect cube factor and the remaining factor.
- Simplify the perfect cube factor by taking its cube root.
💡 Note: This method only works when the radicand has a perfect cube factor.
Method 3: Simplifying Radicals with Coefficients
When a radical has a coefficient (a number in front of the radical), you can simplify it by factoring out the coefficient and the radicand separately.
| Radical | Simplified Form |
|---|---|
| 2√16 | 8 |
| 3∛27 | 9 |
To simplify a radical using this method:
- Factor out the coefficient and the radicand separately.
- Simplify the radical by factoring out perfect squares or perfect cubes.
- Multiply the simplified radical by the coefficient.
Method 4: Simplifying Radicals with Variables
When working with radicals that contain variables, you can simplify them by factoring out the variable and the radicand separately.
| Radical | Simplified Form |
|---|---|
| √(16x^2) | 4x |
| ∛(27x^3) | 3x |
To simplify a radical using this method:
- Factor out the variable and the radicand separately.
- Simplify the radical by factoring out perfect squares or perfect cubes.
- Multiply the simplified radical by the variable.
Method 5: Using the Conjugate to Simplify Radicals
When working with radicals that have a binomial (two-term) radicand, you can simplify them using the conjugate.
| Radical | Simplified Form |
|---|---|
| √(2 + √3) | √(2 + √3) × (√(2 - √3) / (√(2 - √3))) |
To simplify a radical using this method:
- Multiply the radical by its conjugate (the binomial with the opposite sign).
- Simplify the resulting expression by factoring out perfect squares or perfect cubes.
By mastering these five methods, you’ll become proficient in simplifying radicals and unlock the power of this fundamental concept in mathematics.
In summary, simplifying radicals involves factoring out perfect squares, perfect cubes, and coefficients, as well as using the conjugate to simplify radicals with binomial radicands. With practice and patience, you’ll become a pro at simplifying radicals and tackling even the most challenging math problems.
What is a radical?
+A radical is a symbol used to represent the nth root of a number.
What is a perfect square?
+A perfect square is a number that can be expressed as the product of an integer multiplied by itself.
How do I simplify a radical with a coefficient?
+To simplify a radical with a coefficient, factor out the coefficient and the radicand separately, and then simplify the radical.