5 Ways to Master Segment Lengths in Circles
Understanding Segment Lengths in Circles
In geometry, a segment is a part of a line or a curve that connects two points. When it comes to circles, segments can be particularly useful in solving various problems. However, one of the most important concepts to grasp is segment lengths in circles. Mastering segment lengths can help you calculate distances, angles, and other essential properties of a circle.
1. The Power of the Pythagorean Theorem
The Pythagorean Theorem is a fundamental concept in geometry that helps you calculate the length of a segment in a circle. If you have a right triangle inscribed in a circle, you can use the theorem to find the length of the hypotenuse (the segment opposite the right angle). The theorem states that:
a² + b² = c²
where a and b are the lengths of the legs of the triangle, and c is the length of the hypotenuse.
For example, if you have a right triangle with legs of length 3 and 4, you can use the theorem to calculate the length of the hypotenuse:
3² + 4² = c² 9 + 16 = c² 25 = c² c = √25 c = 5
Therefore, the length of the hypotenuse (the segment) is 5 units.
📝 Note: The Pythagorean Theorem only works for right triangles, so make sure you have a right angle in your triangle before applying the theorem.
2. Using the Distance Formula
Another way to calculate segment lengths in circles is by using the distance formula. The distance formula is a general formula that calculates the distance between two points in a coordinate plane. If you have two points on a circle, you can use the distance formula to find the length of the segment connecting them.
The distance formula is:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
where (x₁, y₁) and (x₂, y₂) are the coordinates of the two points, and d is the distance between them.
For example, if you have two points on a circle with coordinates (2, 3) and (4, 6), you can use the distance formula to find the length of the segment connecting them:
d = √((4 - 2)² + (6 - 3)²) d = √(2² + 3²) d = √(4 + 9) d = √13 d ≈ 3.61
Therefore, the length of the segment connecting the two points is approximately 3.61 units.
3. Finding Segment Lengths using Angles
You can also find segment lengths in circles using angles. If you have an angle and the radius of the circle, you can use the sine, cosine, or tangent functions to find the length of the segment.
For example, if you have an angle of 60° and a radius of 4 units, you can use the sine function to find the length of the segment:
sin(60°) = opposite side / hypotenuse sin(60°) = segment length / 4 segment length = 4 * sin(60°) segment length ≈ 4 * 0.866 segment length ≈ 3.46
Therefore, the length of the segment is approximately 3.46 units.
4. Using Segment Addition Postulate
The segment addition postulate states that if two segments share a common endpoint, then the length of the longer segment is equal to the sum of the lengths of the two segments.
For example, if you have two segments with lengths 3 and 4, and they share a common endpoint, then the length of the longer segment is:
3 + 4 = 7
Therefore, the length of the longer segment is 7 units.
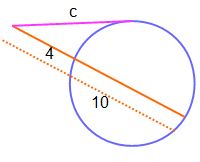
5. Utilizing Circle Properties
Finally, you can use various circle properties to find segment lengths. For example, if you have a chord (a segment that connects two points on a circle) and the radius of the circle, you can use the chord’s length and the radius to find the segment length.
For example, if you have a chord with length 6 units and a radius of 3 units, you can use the Pythagorean Theorem to find the segment length:
3² + 3² = 6² 9 + 9 = 36 18 = 36 6² = 36 - 18 6² = 18 6 = √18 6 ≈ 4.24
Therefore, the length of the segment is approximately 4.24 units.
To master segment lengths in circles, it’s essential to practice using various formulas and properties. By combining these methods, you can solve a wide range of problems and develop a deeper understanding of circle geometry.
In conclusion, mastering segment lengths in circles requires a combination of mathematical formulas and geometric properties. By using the Pythagorean Theorem, distance formula, angles, segment addition postulate, and circle properties, you can solve various problems and develop a deeper understanding of circle geometry.
What is the Pythagorean Theorem?
+The Pythagorean Theorem is a fundamental concept in geometry that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
How do I calculate the length of a segment in a circle?
+There are several ways to calculate the length of a segment in a circle, including using the Pythagorean Theorem, distance formula, angles, segment addition postulate, and circle properties.
What is the segment addition postulate?
+The segment addition postulate states that if two segments share a common endpoint, then the length of the longer segment is equal to the sum of the lengths of the two segments.
Related Terms:
- Segment lengths in Circles formulas
- Circles Worksheet with answers