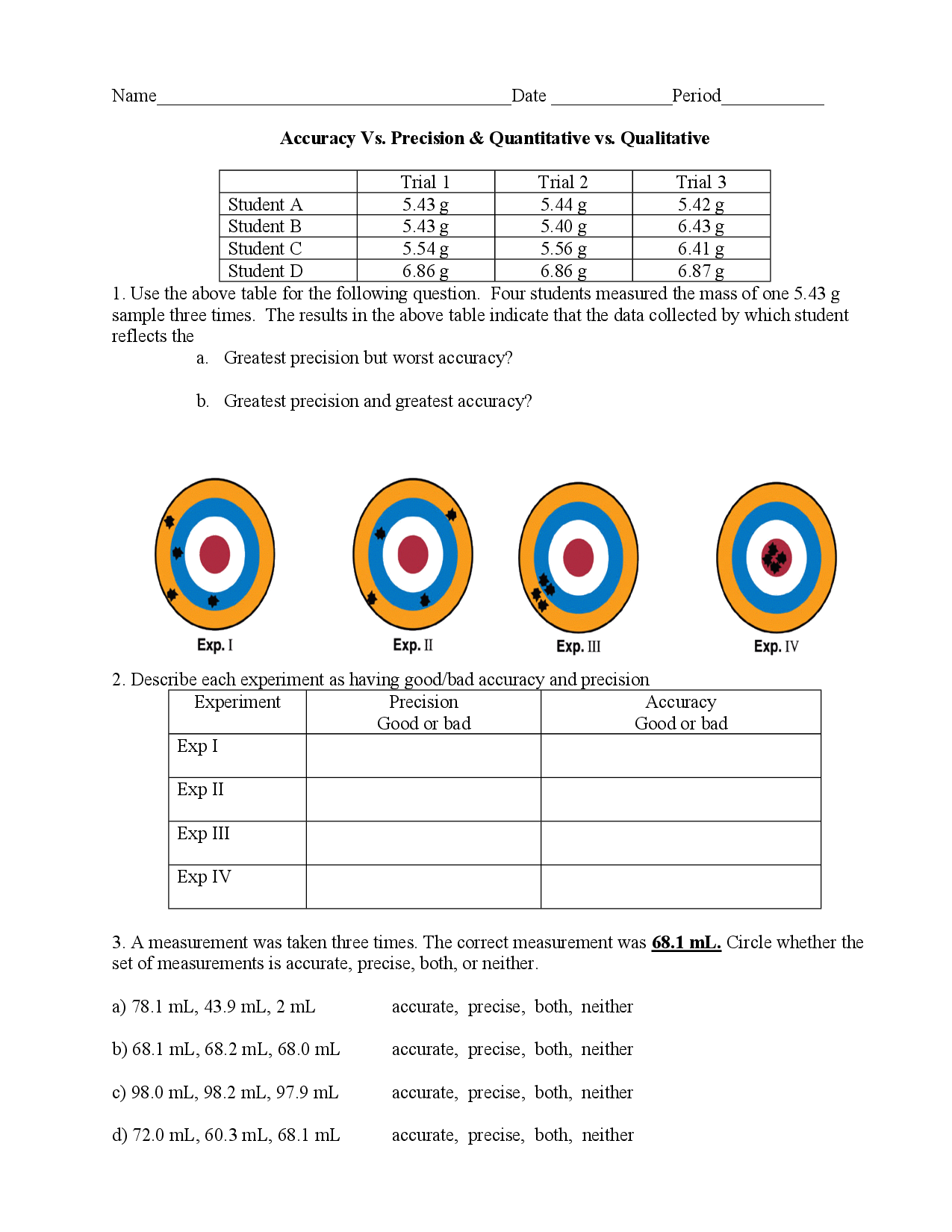
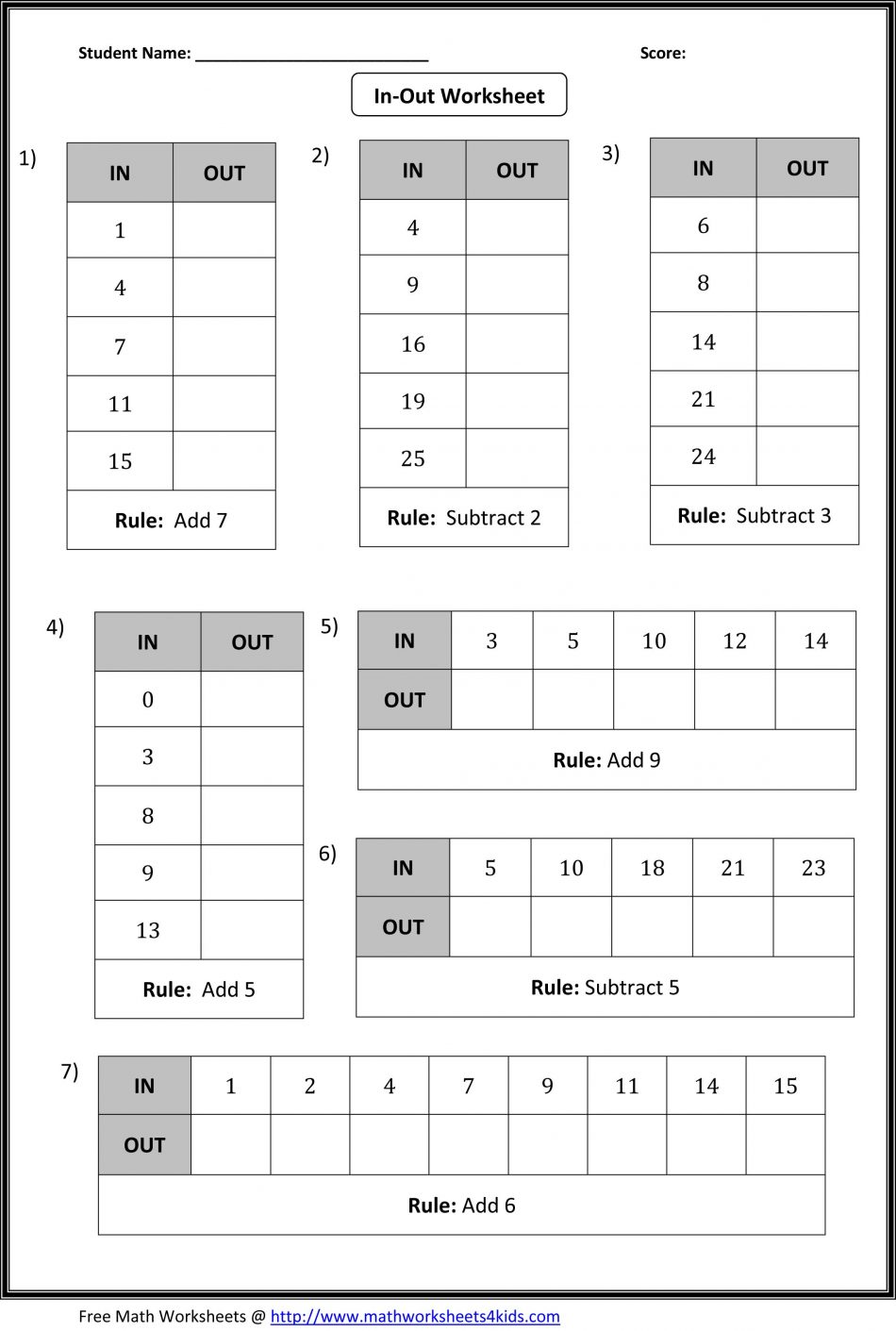
Scientific Notation and Significant Figures Worksheet

Understanding Scientific Notation and Significant Figures

Scientific notation and significant figures are fundamental concepts in science, mathematics, and engineering. They help us express large or small numbers in a more manageable and meaningful way, while also conveying the precision of our measurements. In this worksheet, we will explore the rules and applications of scientific notation and significant figures, with a focus on solving problems and answering questions.

Scientific Notation

Scientific notation is a way of expressing numbers in the form:

a × 10^n

where a is a number between 1 and 10, and n is an integer. This notation is useful for expressing very large or very small numbers in a more compact form.

For example, the number 456,000,000 can be written in scientific notation as:

4.56 × 10^8

To convert a number to scientific notation, we move the decimal point to the left or right until we have a number between 1 and 10. The number of places we move the decimal point is the exponent of 10.

Rules for Scientific Notation:

• The coefficient (a) must be between 1 and 10.
• The exponent (n) must be an integer.
• The base (10) is always implied.

Significant Figures

Significant figures are a way of expressing the precision of a measurement. They indicate the number of digits in a measurement that are reliable and certain.

Rules for Significant Figures:

• Non-zero digits are always significant.
• Zeros between non-zero digits are significant.
• Leading zeros are not significant.
• Trailing zeros are significant only if the number contains a decimal point.

For example, the number 456 has three significant figures, while the number 0.0456 has three significant figures as well.

Applying Scientific Notation and Significant Figures

Now that we have reviewed the rules for scientific notation and significant figures, let’s apply them to some problems.

Problem 1:

Express the number 34,500,000 in scientific notation.

Solution:

Move the decimal point 7 places to the left to get:

3.45 × 10^7

Problem 2:

Round the number 456.789 to three significant figures.

Solution:

Round the number to 457.

Problem 3:

Express the number 0.000456 in scientific notation.

Solution:

Move the decimal point 4 places to the right to get:

4.56 × 10^-4

Problem 4:

Add the numbers 2.34 × 10^5 and 4.56 × 10^4.

Solution:

Convert both numbers to the same exponent (10^5):

2.34 × 10^5 + 0.456 × 10^5 = 2.796 × 10^5

Problem 5:

Multiply the numbers 3.45 × 10^7 and 2.12 × 10^3.

Solution:

Multiply the coefficients and add the exponents:

(3.45 × 2.12) × 10^(7+3) = 7.31 × 10^10

🔍 Note: When multiplying or dividing numbers in scientific notation, the exponents are added or subtracted, respectively.

Problem 6:

Express the result of problem 5 in standard notation.

Solution:

Move the decimal point 10 places to the right to get:

73,100,000,000

Conclusion

Scientific notation and significant figures are powerful tools for expressing and manipulating numbers in science and mathematics. By following the rules and applying these concepts to problems, we can simplify complex calculations and convey the precision of our measurements.