Box Method Worksheet
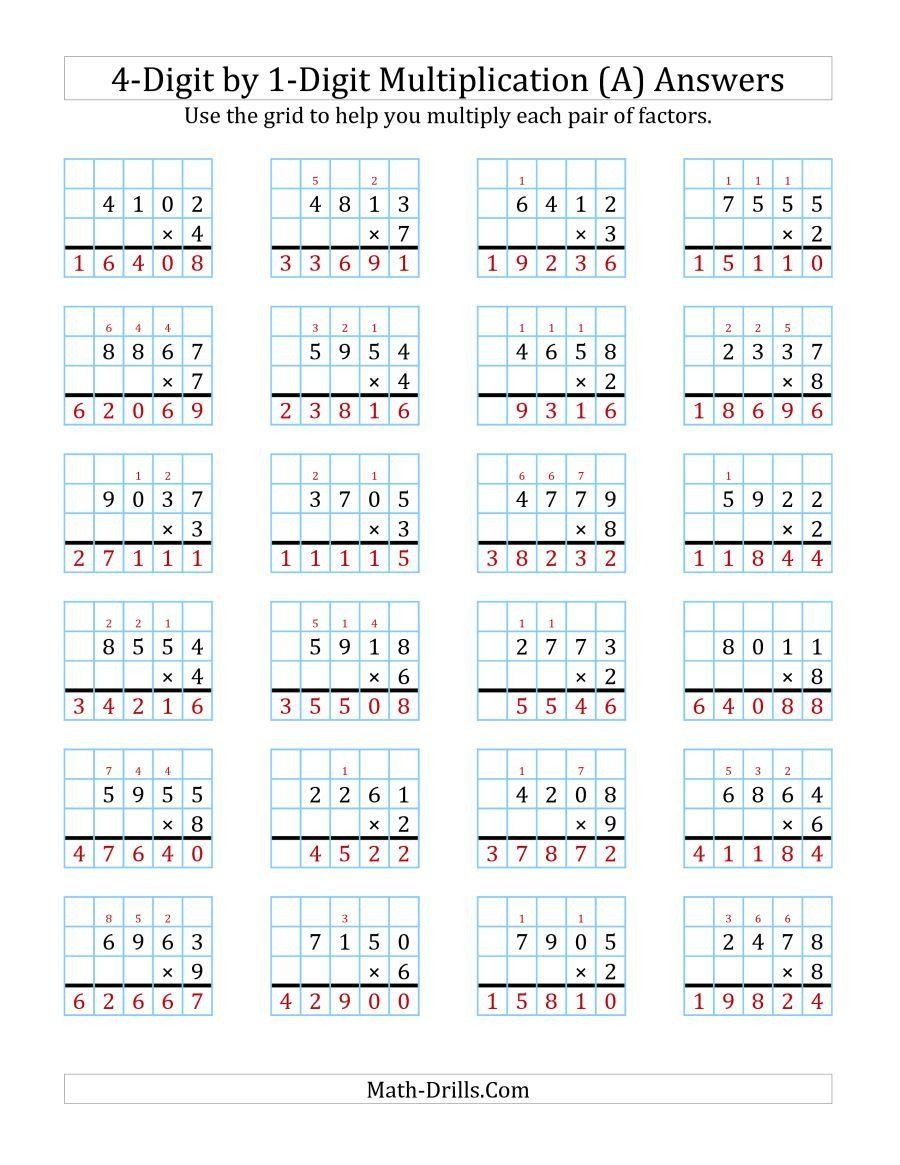
Understanding the Box Method for Multiplication and Division
The box method, also known as the “box multiplication” or “area model,” is a visual representation of multiplication and division that can help students understand the concept of place value and the relationship between numbers. This method is particularly useful for students who struggle with traditional multiplication and division algorithms.
What is the Box Method?
The box method involves using a diagram to represent the multiplication or division problem. The diagram consists of a series of boxes, each representing a digit in the multiplicand (the number being multiplied) or dividend (the number being divided). The boxes are arranged in a grid, with the multiplicand or dividend written on top and the multiplier or divisor written on the side.
How to Use the Box Method for Multiplication
To use the box method for multiplication, follow these steps:
- Write the multiplicand (the number being multiplied) on top of the grid, with each digit in a separate box.
- Write the multiplier (the number by which we are multiplying) on the side of the grid, with each digit in a separate box.
- Multiply each digit in the multiplicand by each digit in the multiplier, writing the product in the corresponding box.
- Add up the products to get the final answer.
Example: 43 × 27
| Tens | Ones | |
|---|---|---|
| 40 | 40 × 20 = 800 | 40 × 7 = 280 |
| 3 | 3 × 20 = 60 | 3 × 7 = 21 |
| 860 | 301 |
Answer: 43 × 27 = 1161
How to Use the Box Method for Division
To use the box method for division, follow these steps:
- Write the dividend (the number being divided) on top of the grid, with each digit in a separate box.
- Write the divisor (the number by which we are dividing) on the side of the grid, with each digit in a separate box.
- Divide each digit in the dividend by each digit in the divisor, writing the quotient in the corresponding box.
- Multiply the quotient by the divisor to check the answer.
Example: 945 ÷ 15
| Tens | Ones | |
|---|---|---|
| 900 | 900 ÷ 10 = 90 | |
| 40 | 40 ÷ 10 = 4 | |
| 5 | 5 ÷ 5 = 1 | |
| 94 | 1 |
Answer: 945 ÷ 15 = 63
Benefits of the Box Method
The box method has several benefits, including:
- Improved understanding of place value: The box method helps students understand the concept of place value and how numbers are represented in different places.
- Visual representation: The box method provides a visual representation of the multiplication or division problem, making it easier for students to understand.
- Breaking down complex problems: The box method helps students break down complex multiplication and division problems into smaller, more manageable parts.
- Developing problem-solving skills: The box method encourages students to think critically and develop problem-solving skills.
Conclusion
The box method is a powerful tool for teaching multiplication and division. By providing a visual representation of the problem, the box method helps students understand the concept of place value and develop problem-solving skills. With practice and patience, students can master the box method and become more confident in their ability to multiply and divide.
Notes
📝 Note: The box method can be adapted to suit different learning styles and abilities.
📝 Note: The box method is not suitable for all types of multiplication and division problems, such as those involving decimals or fractions.
FAQ
What is the box method?
+The box method is a visual representation of multiplication and division that helps students understand the concept of place value and the relationship between numbers.
How do I use the box method for multiplication?
+To use the box method for multiplication, write the multiplicand on top of the grid, with each digit in a separate box, and the multiplier on the side, with each digit in a separate box. Multiply each digit in the multiplicand by each digit in the multiplier, writing the product in the corresponding box.
What are the benefits of the box method?
+The box method has several benefits, including improved understanding of place value, visual representation, breaking down complex problems, and developing problem-solving skills.
Related Terms:
- Teacher synergy llc
- IXL
- Khan Academy
- BrainPOP
- Udacity
- Duolingo