5 Ways to Master Quadratic Functions

Unlocking the Secrets of Quadratic Functions
Quadratic functions are a fundamental concept in mathematics, and mastering them is crucial for success in various fields, including physics, engineering, and computer science. These functions are used to model real-world phenomena, such as the trajectory of a projectile, the shape of a mirror, and the behavior of electrical circuits. In this article, we will explore five ways to master quadratic functions, from understanding the basics to applying them in complex problems.
1. Understand the Basics
A quadratic function is a polynomial function of degree two, which means it can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the value of a. To master quadratic functions, it’s essential to understand the basic concepts, including:
- Vertex form: The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
- Axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex of the parabola and is perpendicular to the x-axis.
- X-intercepts: The x-intercepts are the points where the graph of the quadratic function intersects the x-axis.
📝 Note: The x-intercepts can be found by setting f(x) = 0 and solving for x.
2. Learn to Graph Quadratic Functions
Graphing quadratic functions is a crucial skill to master, as it allows you to visualize the behavior of the function. Here are some tips to help you graph quadratic functions:
- Use the vertex form: The vertex form of a quadratic function makes it easy to identify the vertex and axis of symmetry.
- Identify the x-intercepts: Plot the x-intercepts on the graph to help you draw the parabola.
- Use symmetry: Use the axis of symmetry to help you draw the other half of the parabola.
| Vertex Form | Axis of Symmetry | X-Intercepts |
|---|---|---|
| f(x) = a(x - h)^2 + k | x = h | (x - h)^2 = 0 |
3. Solve Quadratic Equations
Solving quadratic equations is a fundamental skill in mathematics, and there are several methods to do so. Here are a few:
- Factoring: Factoring involves expressing the quadratic equation as a product of two binomials.
- Quadratic formula: The quadratic formula is a general method for solving quadratic equations, which states that x = (-b ± √(b^2 - 4ac)) / 2a.
- Graphing: Graphing involves plotting the quadratic function and finding the x-intercepts.
📝 Note: The quadratic formula is a powerful tool for solving quadratic equations, but it can be time-consuming to use. Try to factor the equation first, and use the quadratic formula only when necessary.
4. Apply Quadratic Functions to Real-World Problems
Quadratic functions have numerous applications in real-world problems, including:
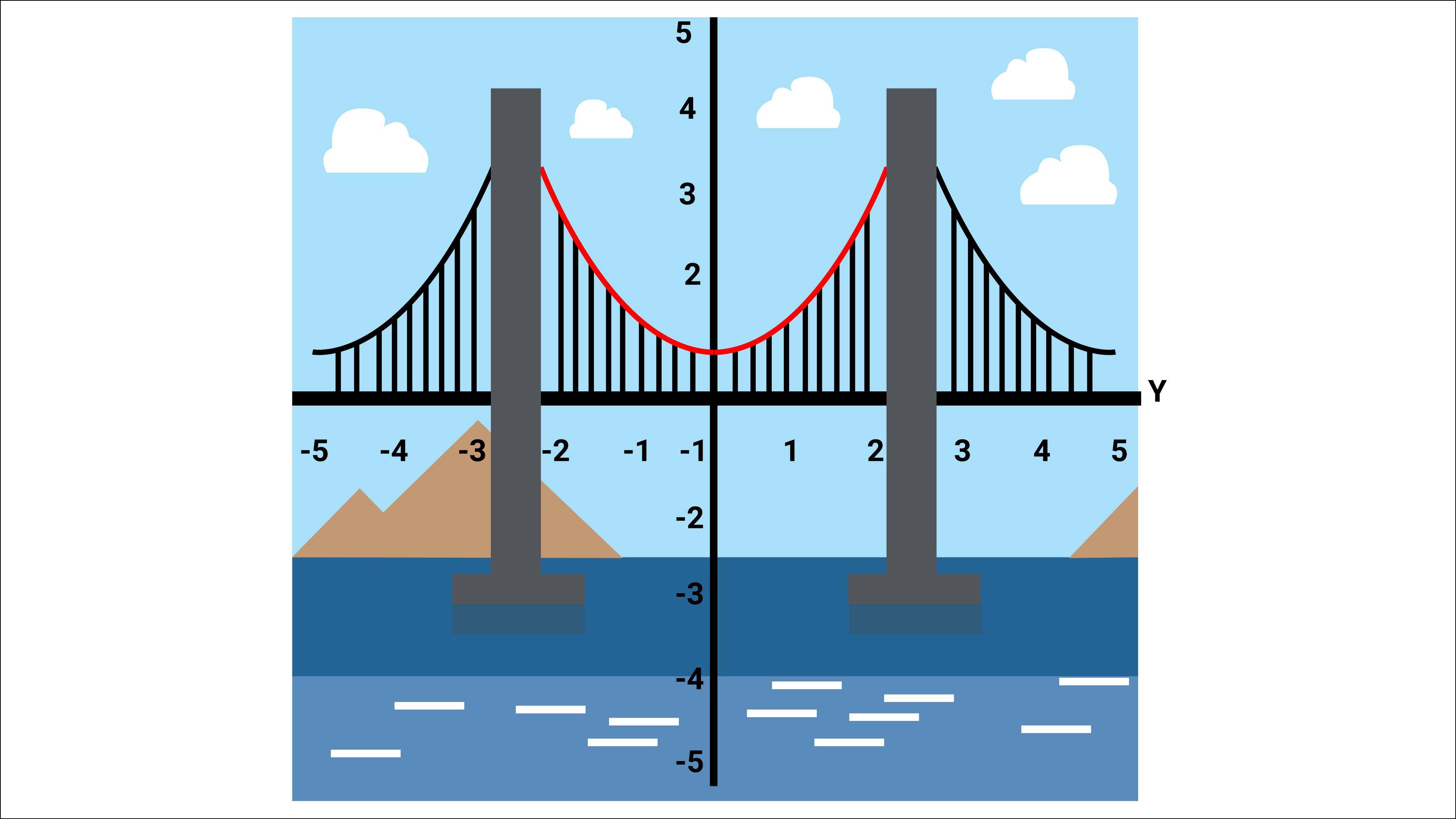
- Projectile motion: Quadratic functions are used to model the trajectory of a projectile, taking into account the initial velocity, angle of projection, and air resistance.
- Electrical circuits: Quadratic functions are used to model the behavior of electrical circuits, including the relationship between voltage, current, and resistance.
- Optics: Quadratic functions are used to model the shape of mirrors and lenses, which are crucial in optics.
5. Practice, Practice, Practice
Mastering quadratic functions requires practice, and there are many resources available to help you do so. Here are a few:
- Online resources: There are many online resources available, including Khan Academy, Mathway, and IXL.
- Textbooks: Textbooks are a great resource for practicing quadratic functions, and they often include worked examples and exercises.
- Practice tests: Practice tests are a great way to assess your knowledge and identify areas for improvement.
As you can see, mastering quadratic functions requires a combination of understanding the basics, learning to graph and solve quadratic equations, applying quadratic functions to real-world problems, and practicing regularly. With dedication and persistence, you can become a master of quadratic functions and unlock the secrets of mathematics.
In the end, mastering quadratic functions is a rewarding experience that will open doors to new opportunities and challenges. By following these five steps, you can develop a deep understanding of quadratic functions and apply them in a variety of contexts.
What is the vertex form of a quadratic function?
+The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
How do I solve a quadratic equation?
+There are several methods to solve a quadratic equation, including factoring, using the quadratic formula, and graphing.
What are some real-world applications of quadratic functions?
+Quadratic functions have numerous applications in real-world problems, including projectile motion, electrical circuits, and optics.