5 Ways to Master Parent Functions Transformations
Mastering Parent Functions Transformations: A Comprehensive Guide
Parent functions are the building blocks of more complex functions, and understanding their transformations is crucial for success in mathematics and other fields. In this article, we will delve into the world of parent functions transformations, exploring five ways to master these essential concepts.
Understanding Parent Functions
Before we dive into transformations, it’s essential to understand what parent functions are. Parent functions are the simplest forms of functions, and they include:
- Linear functions (f(x) = x)
- Quadratic functions (f(x) = x^2)
- Cubic functions (f(x) = x^3)
- Absolute value functions (f(x) = |x|)
- Square root functions (f(x) = √x)
These functions serve as the foundation for more complex functions, and understanding their transformations is vital for problem-solving and critical thinking.
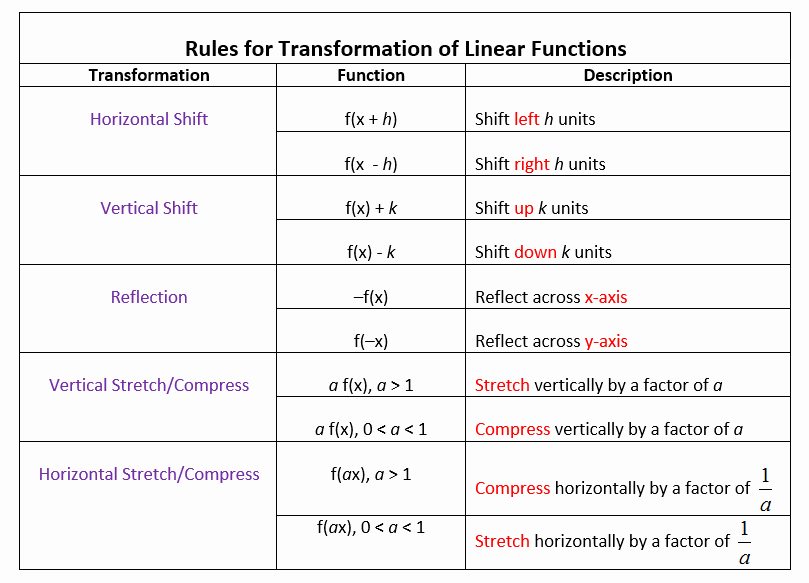
1. Vertical Shifts
A vertical shift occurs when a function is moved up or down by a certain number of units. This type of transformation is denoted by the equation f(x) = af(x) + b, where ‘a’ is the vertical stretch or compression, and ‘b’ is the vertical shift.
- Vertical Stretch: When ‘a’ is greater than 1, the function is stretched vertically, making it taller.
- Vertical Compression: When ‘a’ is between 0 and 1, the function is compressed vertically, making it shorter.
- Vertical Shift: When ‘b’ is added or subtracted, the function is shifted up or down by ‘b’ units.
💡 Note: A vertical shift does not change the shape of the function, only its position.
2. Horizontal Shifts
A horizontal shift occurs when a function is moved left or right by a certain number of units. This type of transformation is denoted by the equation f(x) = f(x - c), where ‘c’ is the horizontal shift.
- Horizontal Shift: When ‘c’ is added or subtracted, the function is shifted left or right by ‘c’ units.
📝 Note: A horizontal shift does not change the shape of the function, only its position.
3. Reflections
A reflection occurs when a function is flipped over a horizontal or vertical axis. This type of transformation is denoted by the equation f(x) = -f(x) for a vertical reflection, and f(x) = f(-x) for a horizontal reflection.
- Vertical Reflection: When a function is reflected over the x-axis, it is flipped upside down.
- Horizontal Reflection: When a function is reflected over the y-axis, it is flipped left to right.
🔄 Note: A reflection does not change the shape of the function, only its orientation.
4. Stretching and Compressing
A stretch or compression occurs when a function is expanded or contracted by a certain factor. This type of transformation is denoted by the equation f(x) = af(x), where ‘a’ is the horizontal stretch or compression.
- Horizontal Stretch: When ‘a’ is greater than 1, the function is stretched horizontally, making it wider.
- Horizontal Compression: When ‘a’ is between 0 and 1, the function is compressed horizontally, making it narrower.
📈 Note: A stretch or compression does not change the shape of the function, only its width.
5. Rotations
A rotation occurs when a function is rotated around a fixed point. This type of transformation is denoted by the equation f(x) = f(x - c) + d, where ‘c’ is the rotation point, and ’d’ is the rotation angle.
- Clockwise Rotation: When a function is rotated clockwise, it is rotated around the origin (0, 0).
- Counterclockwise Rotation: When a function is rotated counterclockwise, it is rotated around the origin (0, 0) in the opposite direction.
🔄 Note: A rotation does not change the shape of the function, only its orientation.
In conclusion, mastering parent functions transformations is essential for problem-solving and critical thinking in mathematics and other fields. By understanding vertical shifts, horizontal shifts, reflections, stretching and compressing, and rotations, you can unlock the secrets of complex functions and tackle even the most challenging problems.
What are parent functions?
+
Parent functions are the simplest forms of functions, including linear, quadratic, cubic, absolute value, and square root functions.
What is a vertical shift?
+
A vertical shift occurs when a function is moved up or down by a certain number of units, denoted by the equation f(x) = af(x) + b.
What is a reflection?
+
A reflection occurs when a function is flipped over a horizontal or vertical axis, denoted by the equation f(x) = -f(x) for a vertical reflection, and f(x) = f(-x) for a horizontal reflection.
Related Terms:
- Function transformations Worksheet Algebra 2