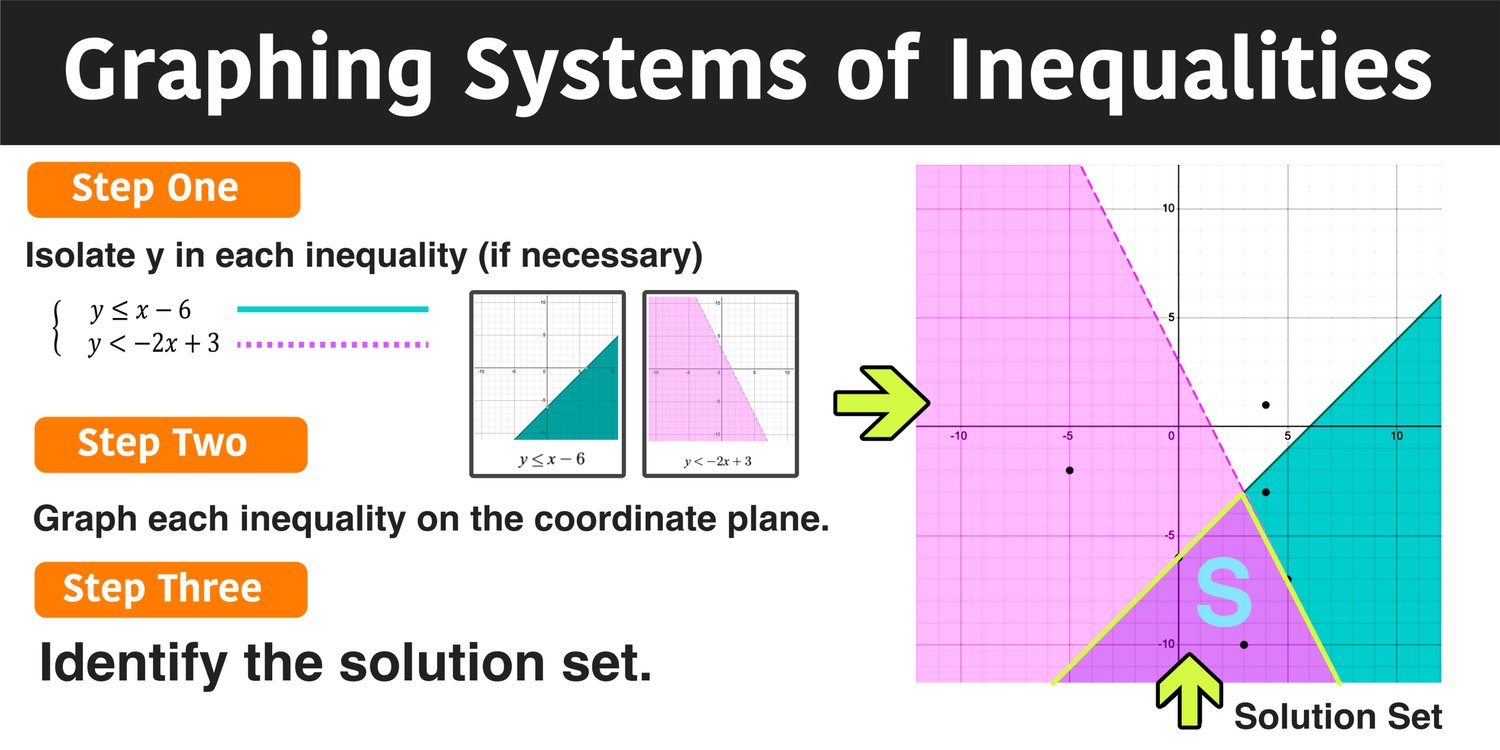
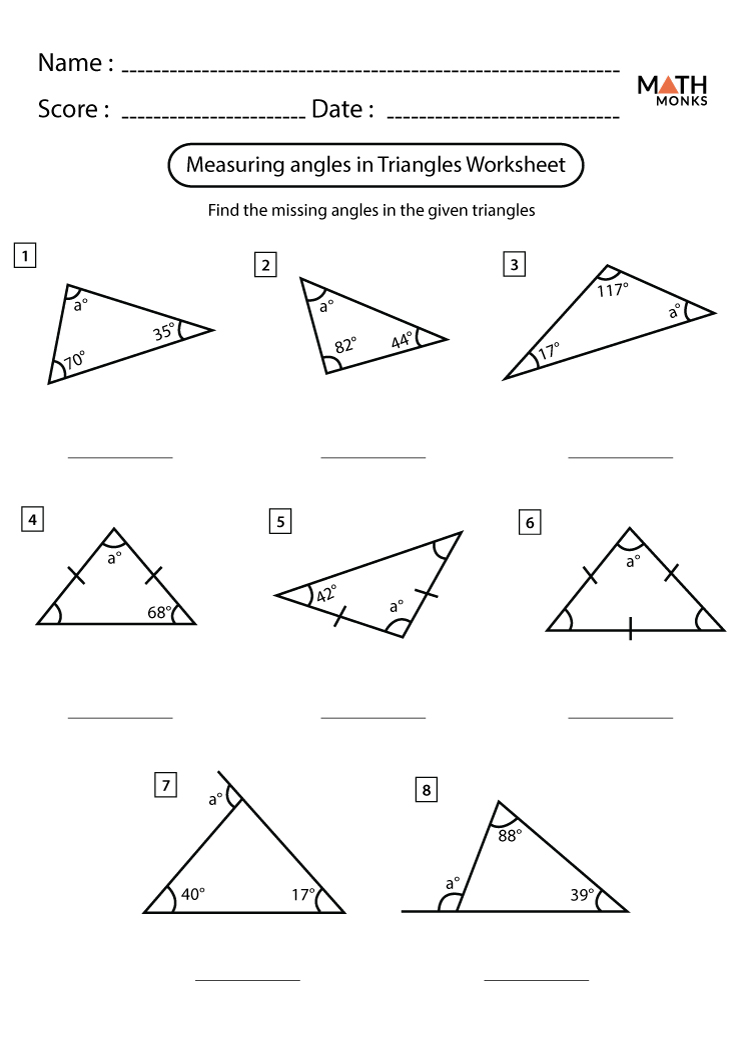
5 Key Properties of Rhombi

Unlocking the Secrets of Rhombi: Exploring 5 Essential Properties
In the realm of geometry, rhombi are a fascinating group of quadrilaterals that possess unique characteristics. A rhombus is a quadrilateral with all sides of equal length. The properties of rhombi make them a crucial part of various mathematical and real-world applications. In this article, we will delve into the 5 key properties of rhombi that every geometry enthusiast should know.
Property 1: All Sides are of Equal Length
One of the most fundamental properties of a rhombus is that all its sides are of equal length. This means that if you were to measure each side of a rhombus, you would get the same value. This property is often denoted as SSSS, where each letter represents a side of equal length.
📝 Note: This property is essential in identifying a rhombus, as it distinguishes it from other types of quadrilaterals.
Property 2: Opposite Angles are Equal
Another critical property of rhombi is that opposite angles are equal. In other words, if you were to measure the angles of a rhombus, you would find that the opposite angles have the same value. This property can be represented as ∠A = ∠C and ∠B = ∠D, where ∠A, ∠B, ∠C, and ∠D are the angles of the rhombus.
🔍 Note: This property is useful in solving problems related to the angles of a rhombus.
Property 3: Diagonals Bisect Each Other at Right Angles
The diagonals of a rhombus bisect each other at right angles, meaning that they intersect at a 90-degree angle. This property can be represented as d₁ ⊥ d₂, where d₁ and d₂ are the diagonals of the rhombus.
📐 Note: This property is essential in finding the area of a rhombus, as it allows us to use the formula: Area = (d₁ × d₂) / 2.
Property 4: Diagonals are Perpendicular to Each Other
The diagonals of a rhombus are perpendicular to each other, meaning that they intersect at a right angle. This property can be represented as d₁ ⋅ d₂ = 0, where d₁ and d₂ are the diagonals of the rhombus.
📊 Note: This property is useful in finding the length of the diagonals of a rhombus.
Property 5: Area of a Rhombus can be Calculated using the Formula
The area of a rhombus can be calculated using the formula: Area = (d₁ × d₂) / 2, where d₁ and d₂ are the diagonals of the rhombus.
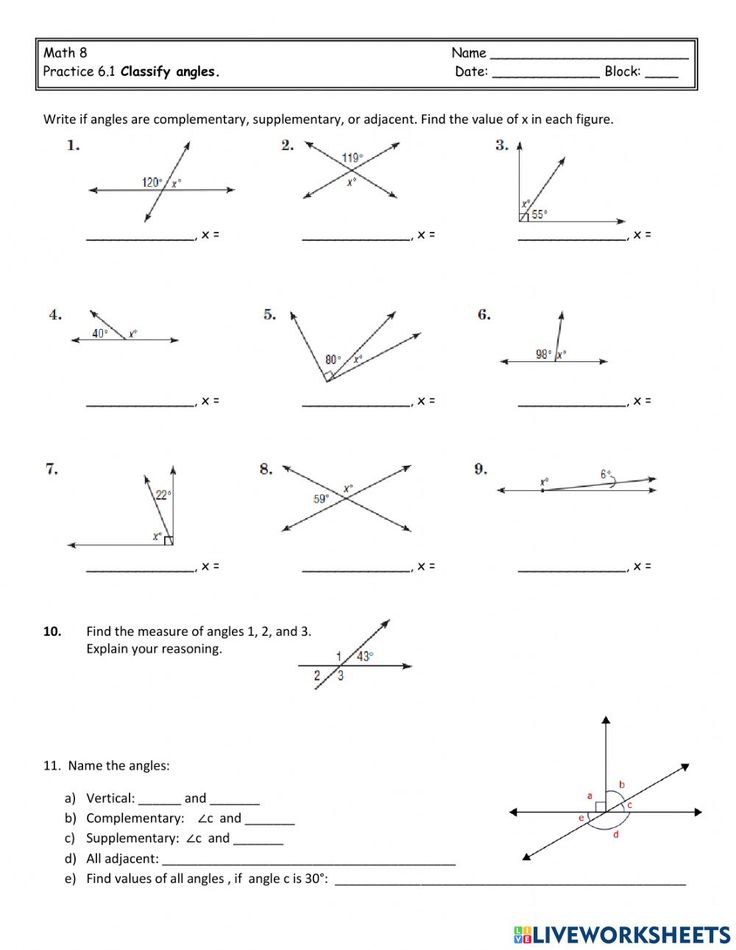
| Diagonal 1 (d₁) | Diagonal 2 (d₂) | Area |
|---|---|---|
| 6 cm | 8 cm | (6 × 8) / 2 = 24 cm² |
📝 Note: This formula is a simple and efficient way to find the area of a rhombus.
By understanding these 5 key properties of rhombi, you will be able to solve problems and apply the concepts to real-world scenarios with ease.
What is a rhombus in geometry?
+A rhombus is a quadrilateral with all sides of equal length.
How do you calculate the area of a rhombus?
+The area of a rhombus can be calculated using the formula: Area = (d₁ × d₂) / 2, where d₁ and d₂ are the diagonals of the rhombus.
What is the difference between a rhombus and a square?
+A rhombus has all sides of equal length, while a square has all sides of equal length and all angles are right angles.
Related Terms:
- Rhombus angles worksheet answers
- Rhombus worksheet preschool
- Properties of rhombus
- Properties of polygons worksheet
- Properties of Squares Worksheet pdf
- Properties of Rectangles worksheet pdf