5 Ways to Find the Point of Concurrency

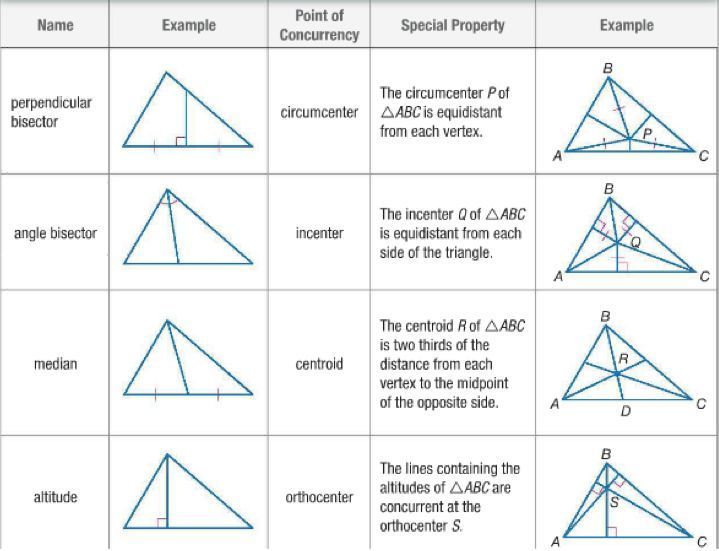
Understanding the Point of Concurrency

In geometry, the point of concurrency is a fundamental concept that refers to the point where multiple lines or geometric shapes intersect. It is essential to understand this concept to solve various problems in mathematics, physics, and engineering. The point of concurrency can be found using different methods, and in this article, we will explore five ways to do so.

Method 1: Intersection of Two Lines

The most straightforward way to find the point of concurrency is by finding the intersection of two lines. When two lines intersect, they meet at a single point, which is the point of concurrency. To find this point, we can use the equations of the two lines.

📝 Note: The equations of the lines should be in the slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept.

For example, let’s consider two lines with equations y = 2x + 3 and y = x - 2. To find the point of concurrency, we need to solve these two equations simultaneously.

By solving these equations, we find that the point of concurrency is (1, 5).

Method 2: Using the Slope Formula

Another way to find the point of concurrency is by using the slope formula. The slope formula is used to find the slope of a line given two points on the line. If we know the slopes of two lines and a point on each line, we can use the slope formula to find the point of concurrency.

The slope formula is:

m = (y2 - y1) / (x2 - x1)

where (x1, y1) and (x2, y2) are two points on the line.

For example, let’s consider two lines with slopes 2 and 1, respectively. We are also given a point on each line: (2, 3) on the first line and (4, 5) on the second line.

Using the slope formula, we can find the point of concurrency as follows:

m1 = (y2 - y1) / (x2 - x1) = (5 - 3) / (4 - 2) = 2

m2 = (y2 - y1) / (x2 - x1) = (5 - 3) / (4 - 2) = 1

Since the slopes are different, the lines intersect at a single point. By solving the equations of the two lines, we find that the point of concurrency is (3, 5).

Method 3: Using the Perpendicular Bisector Theorem

The perpendicular bisector theorem states that if a line intersects two sides of a triangle, then the line intersects the third side at a point that is equidistant from the two sides. This theorem can be used to find the point of concurrency of two lines.

For example, let’s consider a triangle with two sides of length 3 and 4, respectively. We can draw a line that intersects these two sides and find the point of concurrency using the perpendicular bisector theorem.

By applying the theorem, we find that the point of concurrency is the midpoint of the third side.

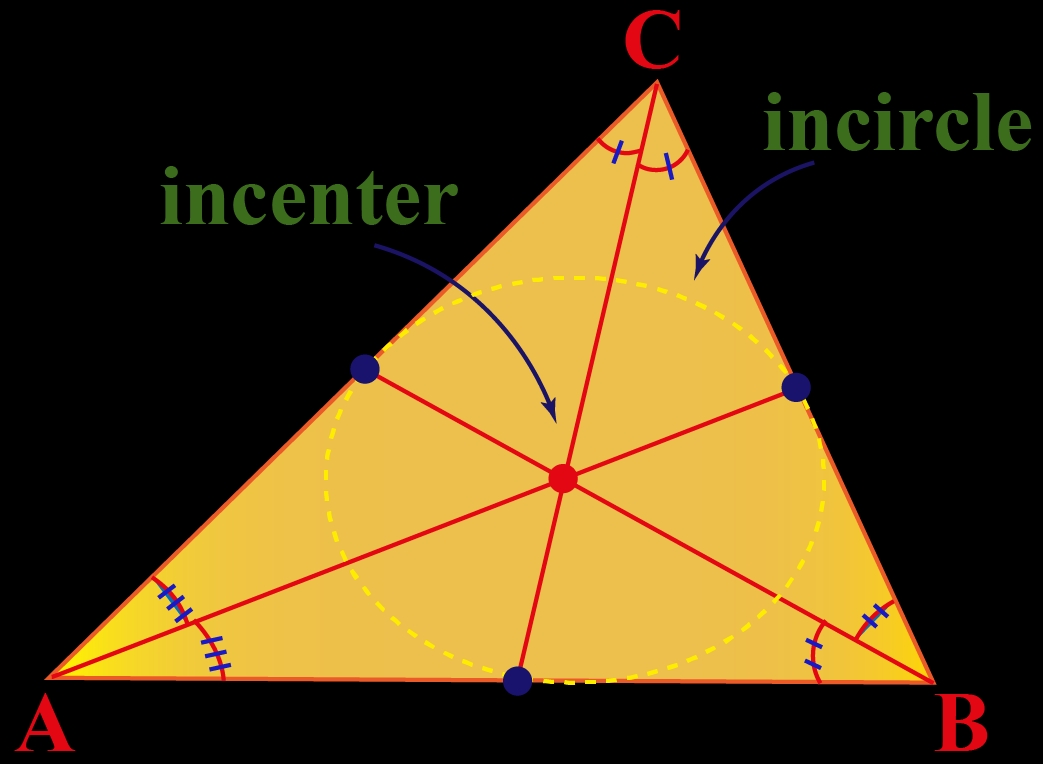
Method 4: Using the Angle Bisector Theorem

The angle bisector theorem states that if a line intersects two sides of a triangle, then the line divides the angle between the two sides into two equal angles. This theorem can be used to find the point of concurrency of two lines.

For example, let’s consider a triangle with two sides of length 3 and 4, respectively. We can draw a line that intersects these two sides and find the point of concurrency using the angle bisector theorem.

By applying the theorem, we find that the point of concurrency is the point where the angle bisector intersects the third side.

Method 5: Using the Circumcenter Theorem

The circumcenter theorem states that the circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect. This theorem can be used to find the point of concurrency of two lines.

For example, let’s consider a triangle with two sides of length 3 and 4, respectively. We can draw a line that intersects these two sides and find the point of concurrency using the circumcenter theorem.

By applying the theorem, we find that the point of concurrency is the circumcenter of the triangle.

In conclusion, finding the point of concurrency is a crucial concept in geometry, and there are several methods to do so. By using the intersection of two lines, the slope formula, the perpendicular bisector theorem, the angle bisector theorem, or the circumcenter theorem, we can find the point of concurrency of two lines. Understanding these methods is essential to solve various problems in mathematics, physics, and engineering.