5 Ways to Master Parent Function Transformations

Mastering Parent Function Transformations: A Comprehensive Guide
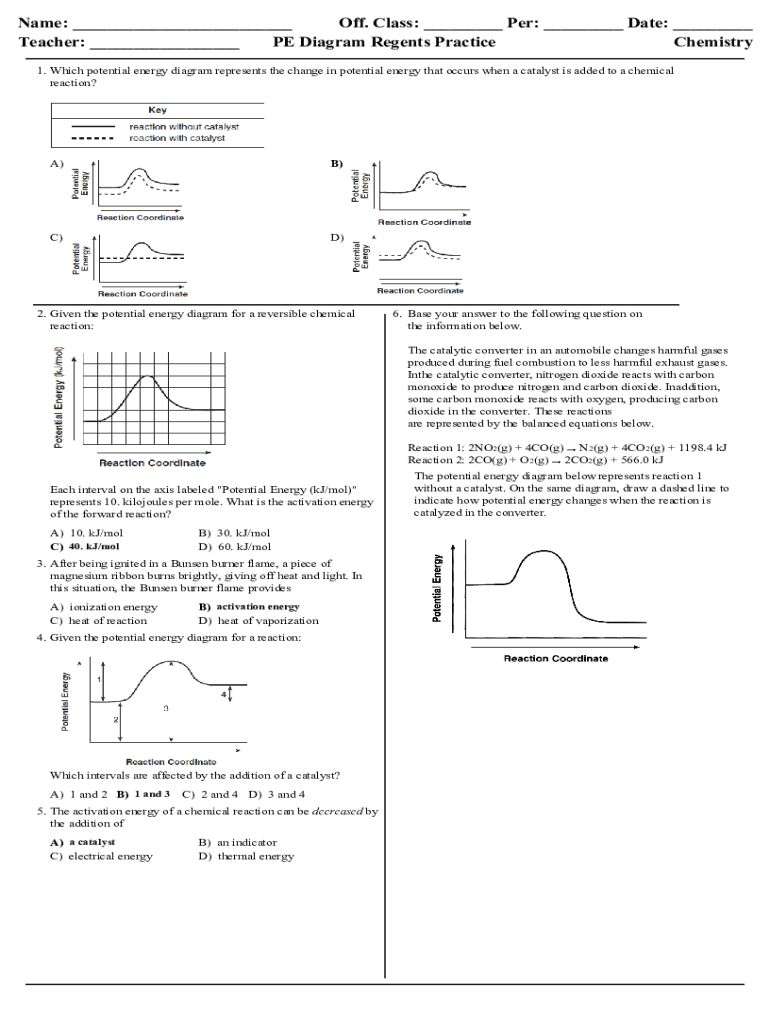
Parent function transformations are a fundamental concept in mathematics, particularly in algebra and geometry. They involve modifying the graph of a parent function to create new functions with different characteristics. Mastering parent function transformations is essential for problem-solving and critical thinking in various mathematical contexts. In this article, we will explore five ways to master parent function transformations, providing you with a solid foundation for understanding and applying these concepts.
Understanding Parent Functions
Before diving into transformations, it’s crucial to understand parent functions. A parent function is a basic function that serves as the foundation for other functions. Common parent functions include linear, quadratic, absolute value, and trigonometric functions. Each parent function has its unique graph, which can be transformed to create new functions.
1. Horizontal and Vertical Shifts
One of the simplest ways to transform a parent function is by applying horizontal and vertical shifts. A horizontal shift involves moving the graph of the parent function left or right by a certain number of units, while a vertical shift involves moving the graph up or down.
Horizontal Shift:
- To shift a parent function horizontally, add or subtract a constant value from the input (x) of the function.
- For example, if you have the parent function f(x) = x^2, shifting it 2 units to the right would result in the new function f(x) = (x - 2)^2.
Vertical Shift:
- To shift a parent function vertically, add or subtract a constant value from the output (y) of the function.
- For example, if you have the parent function f(x) = x^2, shifting it 3 units up would result in the new function f(x) = x^2 + 3.
📝 Note: When applying horizontal and vertical shifts, remember that the direction of the shift affects the sign of the constant value. A positive value shifts the graph to the right or up, while a negative value shifts it to the left or down.
2. Reflections and Rotations
Reflections and rotations are another type of transformation that can be applied to parent functions. A reflection involves flipping the graph of the parent function over a horizontal or vertical axis, while a rotation involves rotating the graph by a certain angle around the origin.
Reflections:
- To reflect a parent function over the x-axis, multiply the output (y) of the function by -1.
- To reflect a parent function over the y-axis, multiply the input (x) of the function by -1.
Rotations:
- To rotate a parent function by 90 degrees clockwise, swap the x and y variables and multiply the new x variable by -1.
- To rotate a parent function by 90 degrees counterclockwise, swap the x and y variables and multiply the new y variable by -1.
🔄 Note: When applying reflections and rotations, remember to adjust the signs and variables accordingly to ensure the correct transformation.
3. Stretches and Compressions
Stretches and compressions involve modifying the graph of a parent function by stretching or compressing it horizontally or vertically. This type of transformation can be achieved by multiplying the input or output of the function by a constant value.
Horizontal Stretch or Compression:
- To stretch a parent function horizontally, multiply the input (x) of the function by a constant value greater than 1.
- To compress a parent function horizontally, multiply the input (x) of the function by a constant value between 0 and 1.
Vertical Stretch or Compression:
- To stretch a parent function vertically, multiply the output (y) of the function by a constant value greater than 1.
- To compress a parent function vertically, multiply the output (y) of the function by a constant value between 0 and 1.
📈 Note: When applying stretches and compressions, remember that the constant value affects the direction and magnitude of the transformation.
4. Function Composition
Function composition involves combining two or more functions to create a new function. This type of transformation can be achieved by substituting the output of one function into the input of another function.
Function Composition:
- To compose two functions, substitute the output of the first function into the input of the second function.
- For example, if you have the functions f(x) = x^2 and g(x) = x + 1, composing them would result in the new function f(g(x)) = (x + 1)^2.
📝 Note: When applying function composition, remember to adjust the input and output variables accordingly to ensure the correct transformation.
5. Real-World Applications
Mastering parent function transformations has numerous real-world applications in fields such as physics, engineering, economics, and computer science. Understanding how to transform parent functions can help you model and analyze complex systems, make predictions, and solve problems.
Real-World Examples:
- Modeling population growth using exponential functions
- Analyzing stock market trends using quadratic functions
- Designing electronic circuits using trigonometric functions
- Optimizing manufacturing processes using linear functions
📊 Note: When applying parent function transformations in real-world contexts, remember to consider the practical implications and limitations of the models and solutions.
Mastering parent function transformations requires practice, patience, and persistence. By following these five ways to master parent function transformations, you’ll be well on your way to becoming proficient in this essential mathematical concept.
In summary, parent function transformations are a fundamental concept in mathematics that can be applied in various contexts. By understanding horizontal and vertical shifts, reflections and rotations, stretches and compressions, function composition, and real-world applications, you’ll be able to master parent function transformations and tackle complex mathematical problems with confidence.
What is a parent function?
+A parent function is a basic function that serves as the foundation for other functions.
What is the difference between a horizontal and vertical shift?
+A horizontal shift involves moving the graph of the parent function left or right, while a vertical shift involves moving the graph up or down.
How do I apply function composition?
+To compose two functions, substitute the output of the first function into the input of the second function.
Related Terms:
- Parent function transformations Worksheet PDF
- Parent function Worksheet 2