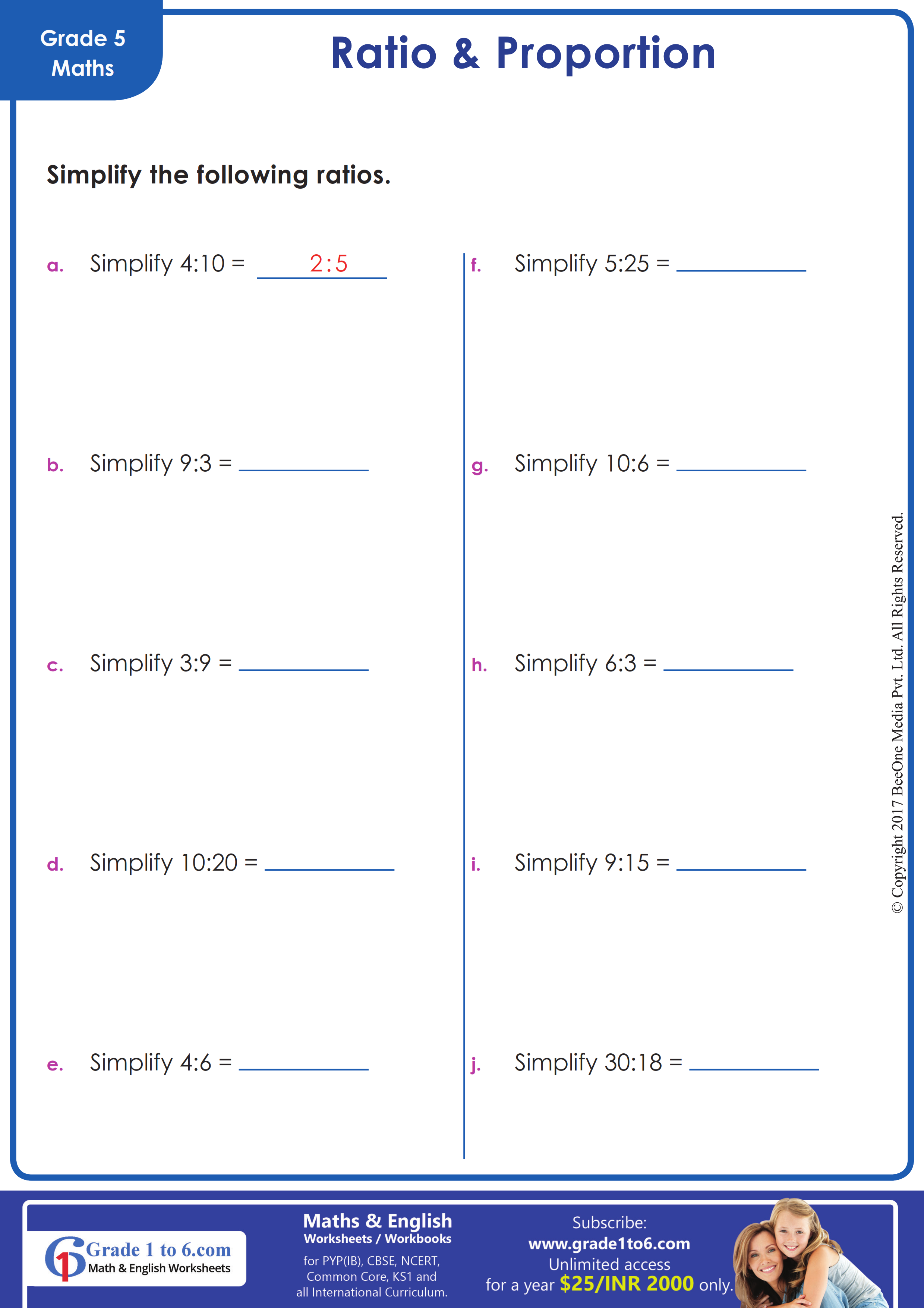
4 Ways to Solve Angles Formed by Secants and Tangents

Understanding Angles Formed by Secants and Tangents

In geometry, secants and tangents are lines that intersect a circle, forming angles that can be challenging to solve. However, with the right strategies, you can master these types of problems. In this article, we will explore four ways to solve angles formed by secants and tangents.

Method 1: Using the Secant-Tangent Theorem

The Secant-Tangent Theorem states that the angle formed by a secant and a tangent line to a circle is equal to half the measure of the intercepted arc. This theorem can be used to solve angles formed by secants and tangents.

Let’s consider an example:

Fig 1: Secant-Tangent Theorem Example

In this example, the angle formed by the secant and tangent lines is equal to half the measure of the intercepted arc, which is 60 degrees. Therefore, the angle is 30 degrees.

📝 Note: The Secant-Tangent Theorem only applies when the secant and tangent lines intersect outside the circle.

Method 2: Using the Angle Bisector Theorem

The Angle Bisector Theorem states that the angle bisector of an angle formed by two secant lines is equal to half the difference of the measures of the intercepted arcs. This theorem can be used to solve angles formed by secants.

Let’s consider an example:

Fig 2: Angle Bisector Theorem Example

In this example, the angle bisector of the angle formed by the two secant lines is equal to half the difference of the measures of the intercepted arcs, which is 30 degrees. Therefore, the angle is 60 degrees.

📝 Note: The Angle Bisector Theorem only applies when the two secant lines intersect inside the circle.

Method 3: Using the Inscribed Angle Theorem

The Inscribed Angle Theorem states that the measure of an angle formed by two chords that intersect inside a circle is equal to half the measure of the intercepted arc. This theorem can be used to solve angles formed by chords that intersect inside a circle.

Let’s consider an example:

Fig 3: Inscribed Angle Theorem Example

In this example, the angle formed by the two chords is equal to half the measure of the intercepted arc, which is 40 degrees. Therefore, the angle is 20 degrees.

Method 4: Using the Properties of Isosceles Triangles

In some cases, the angle formed by a secant and a tangent line can be solved using the properties of isosceles triangles.

Let’s consider an example:

Fig 4: Isosceles Triangle Example

In this example, the triangle formed by the secant and tangent lines is an isosceles triangle, since the two sides that intersect the circle are equal in length. Therefore, the angle formed by the secant and tangent lines is equal to the base angle of the isosceles triangle, which is 45 degrees.

In conclusion, solving angles formed by secants and tangents can be challenging, but by using the right strategies and theorems, you can master these types of problems. Whether it’s using the Secant-Tangent Theorem, the Angle Bisector Theorem, the Inscribed Angle Theorem, or the properties of isosceles triangles, with practice and patience, you can become proficient in solving these types of problems.

Related Terms:

• Tangents Worksheet answer Key