7 Ways to Master Complementary Angles

Understanding Complementary Angles

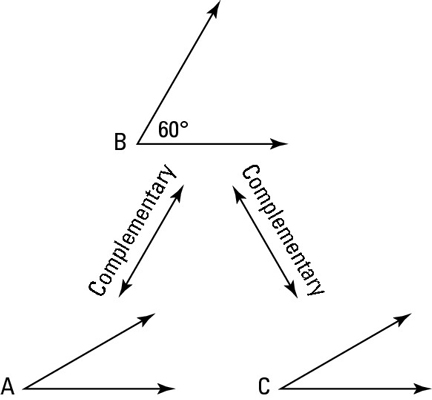
Complementary angles are two angles whose measures add up to 90 degrees. In other words, when you combine two complementary angles, they form a right angle. Mastering complementary angles is essential in various mathematical concepts, including geometry, trigonometry, and algebra. In this article, we will explore seven ways to master complementary angles, making it easier for you to solve problems and understand complex mathematical concepts.

1. Learn the Definition and Properties

To start, it’s crucial to understand the definition and properties of complementary angles. Complementary angles are two angles that add up to 90 degrees. For example, if you have an angle of 30 degrees, its complementary angle would be 60 degrees (90 - 30 = 60). Understanding this basic concept will help you identify complementary angles and apply them in various mathematical problems.

2. Practice Identifying Complementary Angles

Practice makes perfect. Start by identifying complementary angles in different diagrams and problems. You can use a protractor to measure angles and check if they are complementary. The more you practice, the more comfortable you’ll become with identifying complementary angles.

🤔 Note: You can use online resources, such as geometry worksheets or math games, to practice identifying complementary angles.

3. Use Real-World Examples

Complementary angles are not just limited to mathematical problems. They appear in various real-world scenarios, such as:

• Architecture: Complementary angles are used in building designs to create right angles and precise measurements.
• Engineering: Complementary angles are used in mechanical engineering to design and build machines with precise angles.
• Art: Complementary angles are used in art to create balanced and harmonious compositions.

Using real-world examples will help you understand the practical applications of complementary angles.

4. Learn to Calculate Complementary Angles

To calculate complementary angles, you need to know the measure of one angle. If you know the measure of one angle, you can easily calculate the measure of its complementary angle. For example, if you have an angle of 45 degrees, its complementary angle would be 45 degrees (90 - 45 = 45).

5. Use Visual Aids

Visual aids, such as diagrams and charts, can help you understand complementary angles better. Visual aids can help you visualize the relationship between complementary angles. You can use a diagram to show the relationship between two complementary angles and how they add up to 90 degrees.

6. Learn to Apply Complementary Angles in Word Problems

Complementary angles are often used in word problems, where you need to calculate the measure of an angle or the length of a side. Learning to apply complementary angles in word problems will help you solve complex problems. For example:

• “Tom is building a bookshelf with a 30-degree angle on one side. What is the measure of the complementary angle on the other side?”
• “A designer is creating a logo with two complementary angles. If one angle is 45 degrees, what is the measure of the other angle?”

7. Review and Practice Regularly

Mastering complementary angles requires regular review and practice. Set aside time each week to review and practice complementary angles. You can use online resources, such as math games and worksheets, to practice and review complementary angles.

In summary, mastering complementary angles requires a combination of understanding the definition and properties, practicing identification, using real-world examples, learning to calculate complementary angles, using visual aids, applying complementary angles in word problems, and reviewing and practicing regularly. By following these seven ways, you’ll become proficient in complementary angles and be able to solve complex mathematical problems with ease.