Proportional Relationship Worksheet for Math Students
Mastering Proportional Relationships: A Comprehensive Guide for Math Students
Proportional relationships are a fundamental concept in mathematics, and understanding them is crucial for solving various problems in algebra, geometry, and other areas of math. In this article, we will explore the world of proportional relationships, discuss their importance, and provide a worksheet to help math students practice and reinforce their understanding.
What are Proportional Relationships?
A proportional relationship is a relationship between two quantities in which the ratio of one quantity to the other is constant. In other words, as one quantity increases or decreases, the other quantity also increases or decreases at a constant rate. This relationship can be represented by the equation:
y = kx
where y is the dependent variable, x is the independent variable, and k is the constant of proportionality.
Examples of Proportional Relationships
Proportional relationships are all around us, and here are a few examples:
- The cost of buying apples is directly proportional to the number of apples you buy. If you buy 2 apples for 1, the cost of buying 4 apples will be 2, and the cost of buying 6 apples will be $3.
- The distance traveled by a car is directly proportional to the time it travels. If a car travels 100 miles in 2 hours, it will travel 200 miles in 4 hours.
- The area of a circle is directly proportional to the square of its radius. If the radius of a circle is doubled, the area will increase by a factor of 4.
Importance of Proportional Relationships
Understanding proportional relationships is essential for solving various problems in mathematics, science, and real-life situations. Here are a few reasons why:
- Solving algebraic equations: Proportional relationships are used to solve linear equations, which are a crucial part of algebra.
- Analyzing data: Proportional relationships help us analyze data and identify patterns, which is essential in statistics and data analysis.
- Real-life applications: Proportional relationships are used in various real-life applications, such as finance, physics, and engineering.
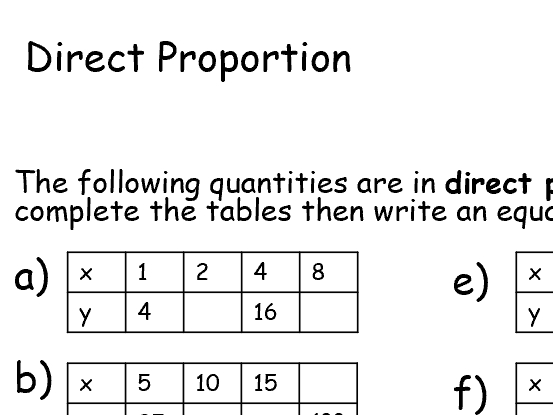
Worksheet: Proportional Relationships
Now that we have discussed the concept of proportional relationships, it’s time to practice! Here’s a worksheet with 10 questions to help you reinforce your understanding:

| Question | A | B | C | D |
|---|---|---|---|---|
| 1. If the cost of buying 2 apples is $1, how much will it cost to buy 6 apples? | $1.50 | $2.50 | $3.00 | $3.50 |
| 2. If a car travels 100 miles in 2 hours, how far will it travel in 5 hours? | 150 miles | 200 miles | 250 miles | 300 miles |
| 3. If the area of a circle with a radius of 4 cm is 16π cm^2, what is the area of a circle with a radius of 6 cm? | 24π cm^2 | 36π cm^2 | 48π cm^2 | 64π cm^2 |
| 4. If a bakery sells 250 loaves of bread at $2 each, how much will it sell 500 loaves of bread for? | $400 | $500 | $600 | $1000 |
| 5. If a car rental company charges $40 per day plus an additional $0.25 per mile, how much will it cost to rent a car for 3 days and drive 200 miles? | $120 | $150 | $180 | $200 |
| 6. If a group of friends want to share some candy equally, and they have 48 pieces of candy to share among 8 friends, how many pieces of candy will each friend get? | 4 pieces | 5 pieces | 6 pieces | 8 pieces |
| 7. If a water tank can hold 1200 liters of water, and 300 liters of water are already in the tank, what percentage of the tank is filled? | 20% | 25% | 30% | 40% |
| 8. If a car travels from City A to City B at an average speed of 60 km/h, and the distance between the two cities is 240 km, how long will the trip take? | 2 hours | 3 hours | 4 hours | 5 hours |
| 9. If a bakery sells 120 cupcakes at $3 each, how much will it sell 240 cupcakes for? | $360 | $480 | $600 | $720 |
| 10. If a person invests $1000 in a savings account that earns 5% interest per year, how much will they have in the account after 2 years? | $1050 | $1100 | $1150 | $1200 |
💡 Note: You can use a calculator to help you with the calculations, but make sure to show your work and explain your reasoning.
Conclusion
In conclusion, proportional relationships are a fundamental concept in mathematics that are used to solve various problems in algebra, geometry, and real-life situations. Understanding proportional relationships is essential for analyzing data, solving linear equations, and making informed decisions. We hope this worksheet has helped you reinforce your understanding of proportional relationships and has provided you with a solid foundation for future math problems.
What is a proportional relationship?
+A proportional relationship is a relationship between two quantities in which the ratio of one quantity to the other is constant.
How are proportional relationships used in real-life situations?
+Proportional relationships are used in various real-life applications, such as finance, physics, and engineering. They help us analyze data, solve problems, and make informed decisions.
What is the formula for a proportional relationship?
+The formula for a proportional relationship is y = kx, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality.