Right Triangle Trigonometry Worksheets for Math Mastery
Unlocking the Secrets of Right Triangle Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. Right triangle trigonometry, in particular, is a fundamental concept that has numerous applications in various fields, including physics, engineering, and computer science. Mastering right triangle trigonometry is crucial for students who want to excel in mathematics and pursue careers in science, technology, engineering, and mathematics (STEM).
In this article, we will explore the world of right triangle trigonometry and provide you with a comprehensive guide to help you master this concept. We will also provide you with worksheets and exercises to help you practice and reinforce your understanding.
Understanding Right Triangle Trigonometry
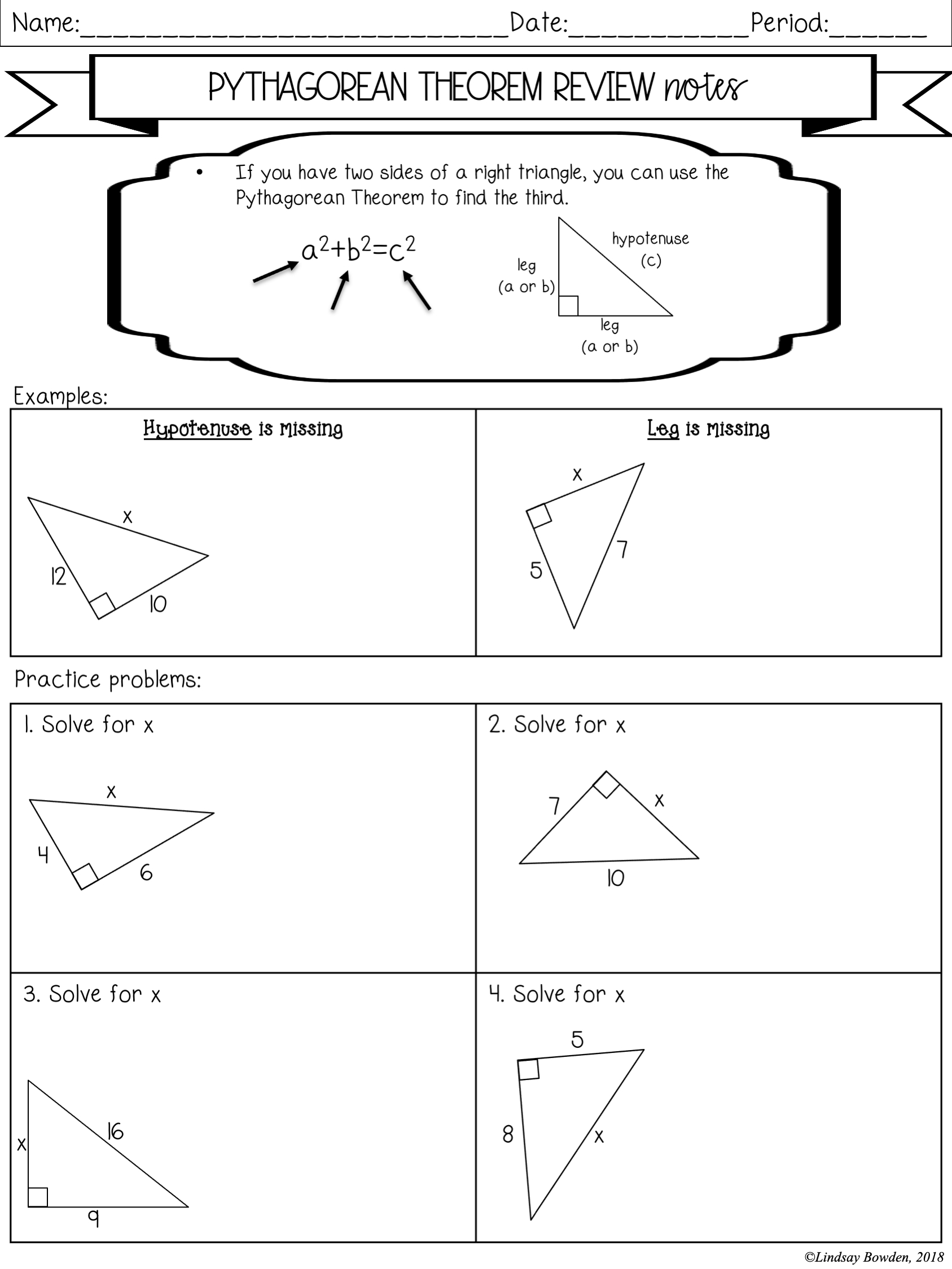
A right triangle is a triangle with one right angle (90 degrees). The trigonometric ratios are defined as the ratios of the lengths of the sides of a right triangle. The three basic trigonometric ratios are:
- Sine (sin): The ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan): The ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
These ratios can be expressed mathematically as:
sin(A) = opposite side / hypotenuse cos(A) = adjacent side / hypotenuse tan(A) = opposite side / adjacent side
Key Concepts and Formulas
Here are some key concepts and formulas that you need to know when working with right triangle trigonometry:
- Pythagorean Theorem: a^2 + b^2 = c^2, where a and b are the lengths of the legs and c is the length of the hypotenuse.
- Trigonometric Identities: sin(A) = cos(90 - A), cos(A) = sin(90 - A), and tan(A) = cot(90 - A)
- Soh-Cah-Toa: A mnemonic device that helps you remember the trigonometric ratios. Sine = Opposite side / Hypotenuse, Cosine = Adjacent side / Hypotenuse, and Tangent = Opposite side / Adjacent side.
Worksheets and Exercises
Here are some worksheets and exercises to help you practice and reinforce your understanding of right triangle trigonometry:
Worksheet 1: Finding Trigonometric Ratios
| Angle | Opposite Side | Adjacent Side | Hypotenuse | sin(A) | cos(A) | tan(A) |
|---|---|---|---|---|---|---|
| 30° | 3 | 4 | 5 | |||
| 45° | 5 | 5 | 7 | |||
| 60° | 7 | 3 | 8 |
Worksheet 2: Solving Right Triangles
| Angle | Opposite Side | Adjacent Side | Hypotenuse |
|---|---|---|---|
| 30° | 6 | 10 | |
| 45° | 8 | 10 | |
| 60° | 6 | 12 |
Worksheet 3: Word Problems
- A ladder leaning against a wall forms a right triangle with the wall and the ground. If the ladder is 10 feet long and the angle between the ladder and the wall is 60°, how far is the base of the ladder from the wall?
- A surveyor measures the angle of elevation to the top of a building and finds it to be 45°. If the distance from the surveyor to the building is 100 feet, how tall is the building?
Practice and Reinforcement
To master right triangle trigonometry, it’s essential to practice and reinforce your understanding regularly. Here are some tips to help you practice effectively:
- Practice regularly: Set aside time each day or week to practice solving right triangle trigonometry problems.
- Use online resources: There are many online resources available that provide practice worksheets, quizzes, and games to help you practice right triangle trigonometry.
- Join a study group: Join a study group or find a study partner to practice and reinforce your understanding of right triangle trigonometry.
👍 Note: Consistency is key when it comes to practicing right triangle trigonometry. Make sure to set aside time each day or week to practice, and you will see improvement over time.
Mastering right triangle trigonometry takes time and practice. With the worksheets and exercises provided in this article, you can reinforce your understanding of this fundamental concept. Remember to practice regularly and use online resources to help you master right triangle trigonometry.
What is the difference between sine, cosine, and tangent?
+
Sine, cosine, and tangent are three basic trigonometric ratios that are defined as the ratios of the lengths of the sides of a right triangle. Sine is the ratio of the length of the side opposite the angle to the length of the hypotenuse, cosine is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse, and tangent is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
How do I find the trigonometric ratios of a right triangle?
+
To find the trigonometric ratios of a right triangle, you need to know the lengths of the sides of the triangle. You can use the formulas sin(A) = opposite side / hypotenuse, cos(A) = adjacent side / hypotenuse, and tan(A) = opposite side / adjacent side to find the trigonometric ratios.
What is the Pythagorean Theorem?
+
The Pythagorean Theorem is a fundamental concept in geometry that states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides. The formula is a^2 + b^2 = c^2, where a and b are the lengths of the legs and c is the length of the hypotenuse.



