Parent Function And Transformation Worksheet

Understanding Parent Functions and Transformations

Parent functions are the simplest form of a function, and they can be transformed to create more complex functions. In this blog post, we will explore the concept of parent functions and transformations, and provide a worksheet to help you practice.

What are Parent Functions?

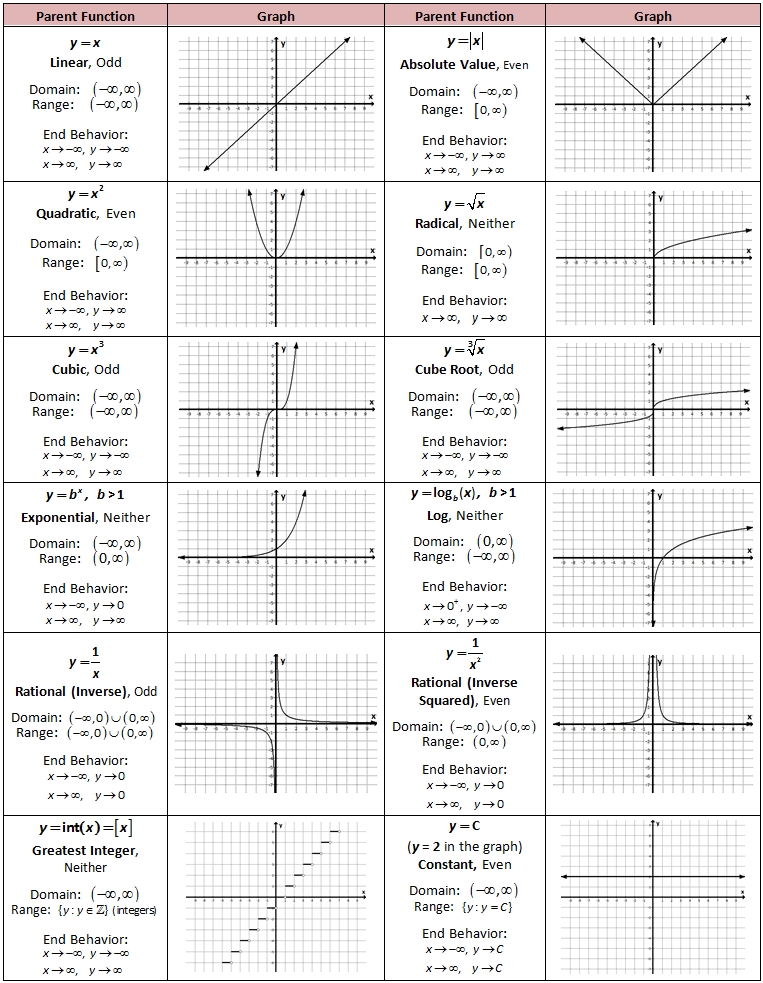
Parent functions are the basic functions that can be transformed to create other functions. They are the simplest form of a function and are used as a starting point for more complex functions. Some common parent functions include:

• Linear functions: f(x) = x
• Quadratic functions: f(x) = x^2
• Cubic functions: f(x) = x^3
• Absolute value functions: f(x) = |x|
• Square root functions: f(x) = √x

Types of Transformations

There are several types of transformations that can be applied to parent functions, including:

• Horizontal Shift: A horizontal shift is a transformation that moves the graph of the function horizontally. For example, if we have a function f(x) = x and we want to shift it 2 units to the right, the new function would be f(x) = x - 2.
• Vertical Shift: A vertical shift is a transformation that moves the graph of the function vertically. For example, if we have a function f(x) = x and we want to shift it 2 units up, the new function would be f(x) = x + 2.
• Horizontal Stretch: A horizontal stretch is a transformation that stretches the graph of the function horizontally. For example, if we have a function f(x) = x and we want to stretch it by a factor of 2, the new function would be f(x) = 2x.
• Vertical Stretch: A vertical stretch is a transformation that stretches the graph of the function vertically. For example, if we have a function f(x) = x and we want to stretch it by a factor of 2, the new function would be f(x) = 2x.
• Reflection: A reflection is a transformation that reflects the graph of the function across the x-axis or y-axis. For example, if we have a function f(x) = x and we want to reflect it across the x-axis, the new function would be f(x) = -x.

Transforming Parent Functions

To transform a parent function, we can apply one or more of the transformations listed above. For example, if we have a parent function f(x) = x^2 and we want to shift it 2 units to the right and stretch it by a factor of 2, the new function would be f(x) = 2(x - 2)^2.

📝 Note: When transforming a parent function, we can apply multiple transformations in any order. However, the order in which we apply the transformations can affect the final result.

Worksheet

Here is a worksheet to help you practice transforming parent functions:

Transformations Worksheet

1. Transform the parent function f(x) = x^2 by shifting it 3 units to the left and stretching it by a factor of 3.
2. Transform the parent function f(x) = |x| by reflecting it across the y-axis and shifting it 2 units up.
3. Transform the parent function f(x) = √x by stretching it by a factor of 2 and shifting it 1 unit to the right.
4. Transform the parent function f(x) = x^3 by reflecting it across the x-axis and shifting it 2 units down.
5. Transform the parent function f(x) = x by stretching it by a factor of 2 and shifting it 1 unit to the left.

Answers

1. f(x) = 3(x + 3)^2
2. f(x) = -|x| + 2
3. f(x) = 2√(x - 1)
4. f(x) = -(x + 2)^3
5. f(x) = 2(x - 1)

Conclusion

In this blog post, we have explored the concept of parent functions and transformations. We have seen how parent functions can be transformed to create more complex functions, and we have provided a worksheet to help you practice. By understanding parent functions and transformations, you can create a wide range of functions and solve complex problems.