6 Ways to Master Parallel Lines Cut by Transversal
Mastering parallel lines cut by a transversal is a fundamental concept in geometry that can help you solve a variety of problems. It’s essential to understand the relationships between the angles formed when a transversal intersects two parallel lines. Here are six ways to help you master this concept:
Understanding the Basics
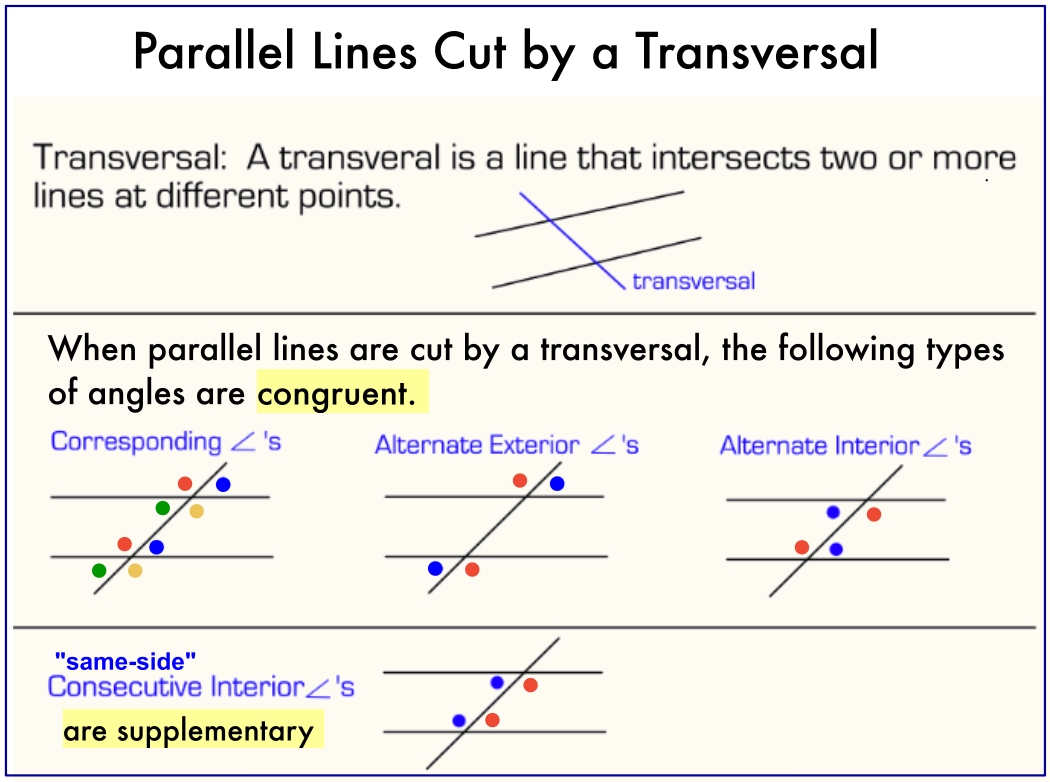
Before diving into the six ways to master parallel lines cut by a transversal, let’s review the basics. When two parallel lines are cut by a transversal, eight angles are formed. These angles can be classified into three types:
- Corresponding angles: These are angles that are in the same relative position in each intersection. For example, ∠1 and ∠5 are corresponding angles.
- Alternate interior angles: These are angles that are on opposite sides of the transversal and inside the parallel lines. For example, ∠2 and ∠6 are alternate interior angles.
- Alternate exterior angles: These are angles that are on opposite sides of the transversal and outside the parallel lines. For example, ∠1 and ∠7 are alternate exterior angles.
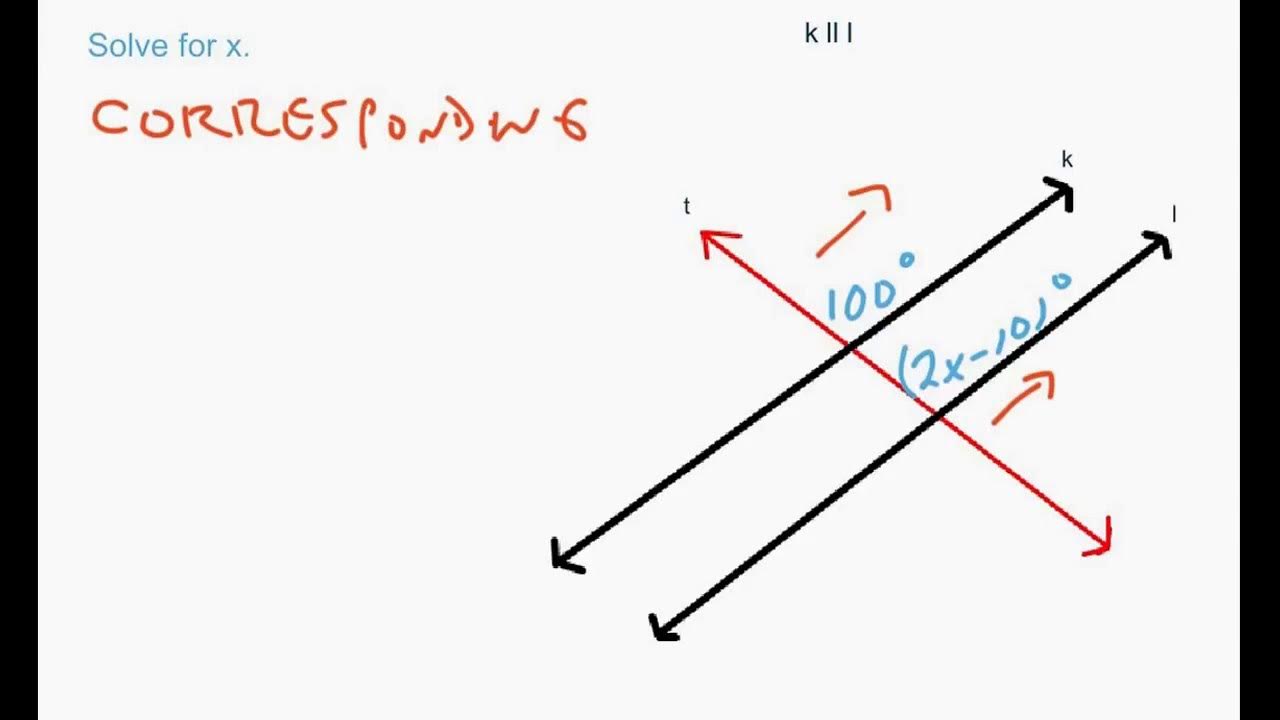
Way 1: Identify Corresponding Angles
To master parallel lines cut by a transversal, start by identifying the corresponding angles. Since corresponding angles are equal, you can use this property to find missing angles. For example:
| ∠1 | ∠2 | ∠3 | ∠4 | ∠5 | ∠6 | ∠7 | ∠8 |
|---|---|---|---|---|---|---|---|
| x | 2x | x | 2x | x | 2x | x | 2x |
If ∠1 = 30°, then ∠5 = 30° because they are corresponding angles.
📝 Note: Make sure to identify the corresponding angles first, as this will help you find the missing angles more easily.
Way 2: Use Alternate Interior Angles
Alternate interior angles are also equal, so you can use this property to find missing angles. For example:
If ∠2 = 45°, then ∠6 = 45° because they are alternate interior angles.
Way 3: Apply Alternate Exterior Angles
Alternate exterior angles are equal, so you can use this property to find missing angles. For example:
If ∠1 = 30°, then ∠7 = 30° because they are alternate exterior angles.
Way 4: Identify Vertical Angles
Vertical angles are angles that are opposite each other and formed by two intersecting lines. When a transversal intersects two parallel lines, the vertical angles are equal. For example:
If ∠1 = 30°, then ∠4 = 30° because they are vertical angles.
Way 5: Use the Linear Pair Theorem
The Linear Pair Theorem states that the sum of the measures of two adjacent angles formed by a transversal intersecting two parallel lines is 180°. For example:
If ∠1 = 30°, then ∠2 = 150° because they are a linear pair.
Way 6: Practice, Practice, Practice!
The best way to master parallel lines cut by a transversal is to practice solving problems. Start with simple problems and gradually move on to more complex ones. You can find many resources online, such as worksheets and practice tests, to help you practice.
By following these six ways, you’ll be well on your way to mastering parallel lines cut by a transversal.
What is the difference between corresponding angles and alternate interior angles?
+Corresponding angles are angles that are in the same relative position in each intersection, while alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines.
How do I identify vertical angles?
+Vertical angles are angles that are opposite each other and formed by two intersecting lines. When a transversal intersects two parallel lines, the vertical angles are equal.
What is the Linear Pair Theorem?
+The Linear Pair Theorem states that the sum of the measures of two adjacent angles formed by a transversal intersecting two parallel lines is 180°.