5 Ways to Master Parallel and Perpendicular Lines
Understanding Parallel and Perpendicular Lines
Parallel and perpendicular lines are fundamental concepts in geometry and are used to describe the relationship between two lines. Parallel lines are lines that lie in the same plane and never intersect, while perpendicular lines are lines that intersect at a right angle (90 degrees). Mastering these concepts is crucial for solving problems in mathematics, physics, engineering, and architecture. In this article, we will explore five ways to master parallel and perpendicular lines.
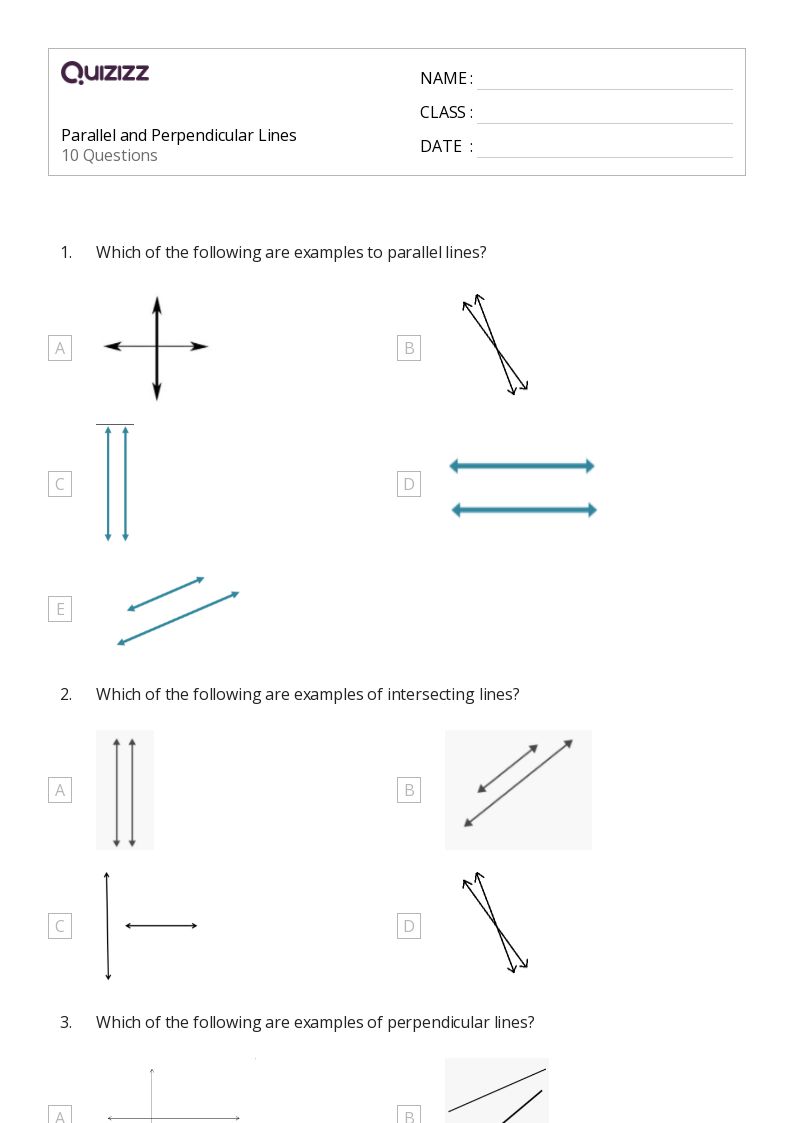
1. Visualizing Parallel and Perpendicular Lines
Visualizing parallel and perpendicular lines is essential to understanding their properties. Parallel lines can be visualized as two lines that never touch or intersect, no matter how far they are extended. Perpendicular lines, on the other hand, can be visualized as two lines that intersect at a right angle, forming an “L” shape.
To visualize parallel and perpendicular lines, try drawing two lines on a piece of paper. For parallel lines, draw two lines that never touch or intersect. For perpendicular lines, draw two lines that intersect at a right angle.
📝 Note: Use a ruler or a straightedge to draw the lines, ensuring they are straight and accurate.
2. Understanding the Properties of Parallel and Perpendicular Lines
Parallel and perpendicular lines have distinct properties that can be used to identify them. Parallel lines have the following properties:
- They never intersect, no matter how far they are extended.
- They have the same slope, but the y-intercept is different.
- They are always the same distance apart.
Perpendicular lines, on the other hand, have the following properties:
- They intersect at a right angle (90 degrees).
- They have different slopes, and the product of their slopes is -1.
- They form a right angle, which can be used to solve problems involving right triangles.
3. Using Slope to Identify Parallel and Perpendicular Lines
Slope is a measure of how steep a line is and can be used to identify parallel and perpendicular lines. Parallel lines have the same slope, but the y-intercept is different. Perpendicular lines, on the other hand, have different slopes, and the product of their slopes is -1.
To identify parallel and perpendicular lines using slope, follow these steps:
- Find the slope of the first line (m1).
- Find the slope of the second line (m2).
- If m1 = m2, the lines are parallel.
- If m1 × m2 = -1, the lines are perpendicular.
4. Applying Parallel and Perpendicular Lines to Real-World Problems
Parallel and perpendicular lines are used in various real-world applications, including architecture, engineering, and physics. Parallel lines are used to design buildings, bridges, and roads, while perpendicular lines are used to design right triangles and solve problems involving right angles.
To apply parallel and perpendicular lines to real-world problems, follow these steps:
- Identify the problem and the type of line involved (parallel or perpendicular).
- Use the properties of parallel and perpendicular lines to solve the problem.
- Apply the solution to the real-world problem.
5. Practicing with Examples and Exercises
Practicing with examples and exercises is essential to mastering parallel and perpendicular lines. Practice problems can be found in mathematics textbooks or online resources.
To practice with examples and exercises, follow these steps:
- Find practice problems involving parallel and perpendicular lines.
- Read the problem carefully and identify the type of line involved.
- Use the properties of parallel and perpendicular lines to solve the problem.
- Check the solution and repeat the process until you feel confident.

| Line Type | Properties | Examples |
|---|---|---|
| Parallel Lines | Same slope, different y-intercept | y = 2x + 1, y = 2x + 3 |
| Perpendicular Lines | Different slopes, product of slopes = -1 | y = 2x + 1, y = -1/2x + 3 |
By following these five ways to master parallel and perpendicular lines, you can develop a deeper understanding of these fundamental concepts and improve your problem-solving skills in mathematics and other fields.
In conclusion, mastering parallel and perpendicular lines requires a combination of visualization, understanding of properties, using slope, applying to real-world problems, and practicing with examples and exercises. By following these steps, you can develop a strong foundation in geometry and improve your problem-solving skills.
What is the difference between parallel and perpendicular lines?
+Parallel lines are lines that never intersect, while perpendicular lines are lines that intersect at a right angle (90 degrees).
How can I identify parallel and perpendicular lines using slope?
+If the slopes of two lines are equal, they are parallel. If the product of their slopes is -1, they are perpendicular.
What are some real-world applications of parallel and perpendicular lines?
+Parallel lines are used in architecture, engineering, and road design, while perpendicular lines are used in right triangles and physics problems.
Related Terms:
- Gradient of perpendicular lines
- Line line segment ray worksheet
- Worksheet angles Grade 3
- Linear graph Worksheet pdf
- Worksheet transformations geometry
- Angles Worksheet