Solving Systems of Equations by Graphing Made Easy
Understanding the Basics of Graphing Systems of Equations
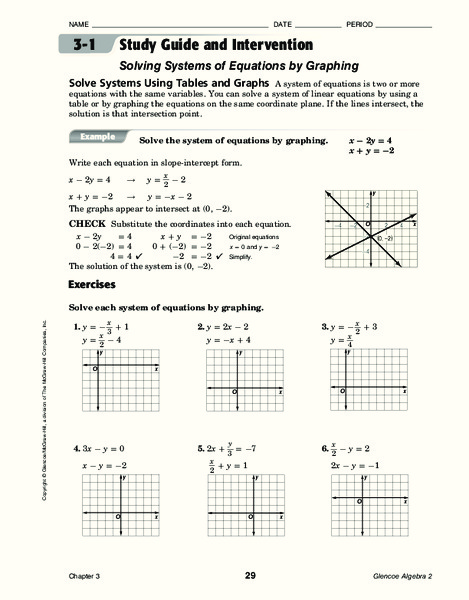
When dealing with systems of equations, it’s essential to have a solid grasp of the concept of graphing. Graphing systems of equations involve plotting two or more equations on the same coordinate plane and finding the point(s) of intersection. This point of intersection represents the solution to the system of equations. In this article, we’ll delve into the world of graphing systems of equations and explore the steps to solve them efficiently.
What is a System of Equations?
A system of equations is a collection of two or more equations that contain the same variables. These equations can be linear or nonlinear, and they may have one or more solutions. A system of equations can be represented in various forms, including:
- Linear System: A system of linear equations, where each equation is in the form of ax + by = c.
- Nonlinear System: A system of nonlinear equations, where each equation is in the form of ax^2 + by^2 = c.
Why Graphing Systems of Equations is Important
Graphing systems of equations is a powerful tool for solving these equations. By visualizing the equations on a coordinate plane, you can easily identify the point(s) of intersection, which represent the solution(s) to the system. Graphing also helps to:
- Identify the number of solutions: By graphing the equations, you can determine if the system has one solution, no solution, or infinitely many solutions.
- Visualize the relationships: Graphing allows you to see the relationships between the variables and how they interact with each other.
Step-by-Step Guide to Graphing Systems of Equations
To graph a system of equations, follow these steps:
- Graph the first equation: Plot the first equation on the coordinate plane. Make sure to label the x and y axes.
- Graph the second equation: Plot the second equation on the same coordinate plane. Make sure to use a different color or symbol to distinguish between the two equations.
- Find the point of intersection: Identify the point where the two graphs intersect. This point represents the solution to the system of equations.
- Check for multiple solutions: If the graphs intersect at more than one point, then the system has multiple solutions.
- Verify the solution: Plug the solution back into both original equations to verify that it satisfies both equations.
📝 Note: When graphing systems of equations, it's essential to use a ruler or a graphing calculator to ensure accuracy.
Examples of Graphing Systems of Equations
Let’s consider two examples:
Example 1:
System of Equations:
2x + 3y = 7 x - 2y = -3
Solution:
Graph the two equations on the same coordinate plane.
Point of intersection: (-1, 2)
This point represents the solution to the system of equations.
Example 2:
System of Equations:
x^2 + y^2 = 4 x - 2y = -1
Solution:
Graph the two equations on the same coordinate plane.
Point of intersection: (1, 1)
This point represents the solution to the system of equations.
Common Challenges and Solutions
When graphing systems of equations, you may encounter some common challenges. Here are some solutions:
- Difficulty finding the point of intersection: Use a graphing calculator or a ruler to help you find the point of intersection accurately.
- Multiple solutions: If the graphs intersect at more than one point, then the system has multiple solutions. Verify each solution by plugging it back into both original equations.
- No solution: If the graphs do not intersect, then the system has no solution.
Conclusion
Graphing systems of equations is a powerful tool for solving these equations. By following the steps outlined in this article, you can easily graph systems of equations and find the point(s) of intersection, which represent the solution(s) to the system. Remember to use a ruler or graphing calculator to ensure accuracy and verify each solution by plugging it back into both original equations.
What is a system of equations?
+A system of equations is a collection of two or more equations that contain the same variables.
Why is graphing systems of equations important?
+Graphing systems of equations helps to identify the number of solutions, visualize the relationships between the variables, and find the point(s) of intersection, which represent the solution(s) to the system.
How do I verify the solution to a system of equations?
+Plug the solution back into both original equations to verify that it satisfies both equations.
Related Terms:
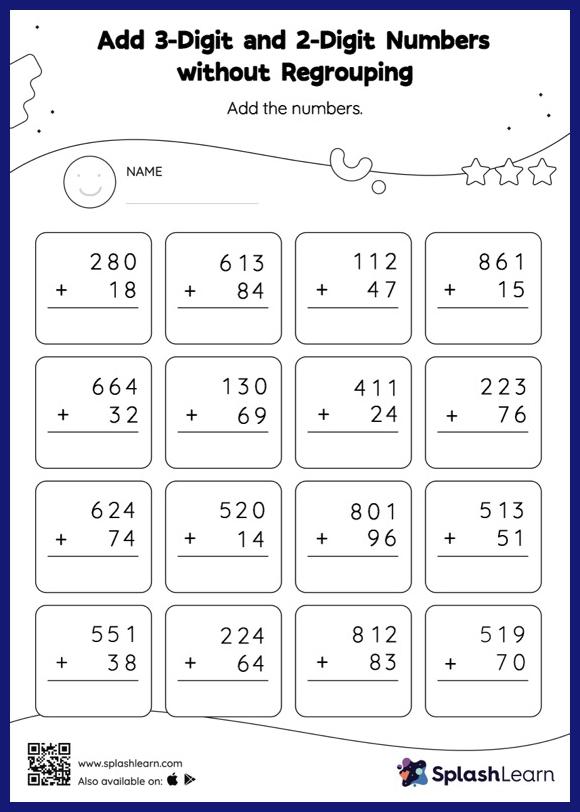
- Solving Systems of equations worksheet