Order of Operations Worksheet No Exponents Practice Tests

Mastering the Order of Operations: A Comprehensive Guide with Practice Tests

The order of operations is a fundamental concept in mathematics that ensures calculations are performed in a consistent and accurate manner. It is a crucial skill to master, especially when working with complex mathematical expressions. In this guide, we will delve into the world of order of operations, explore the rules and conventions, and provide practice tests to help you reinforce your understanding.

What is the Order of Operations?

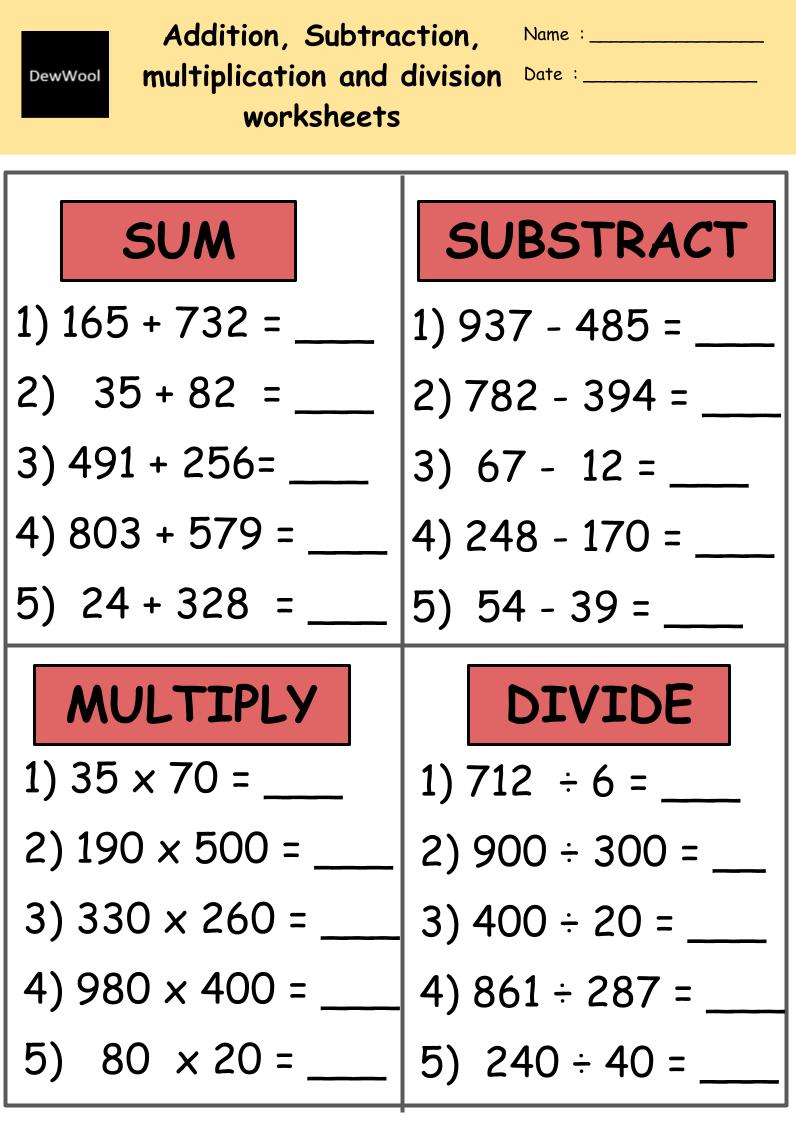
The order of operations is a set of rules that dictates the order in which mathematical operations should be performed when there are multiple operations in an expression. The acronym PEMDAS is commonly used to remember the order of operations:

• Parentheses: Evaluate expressions inside parentheses first.
• Exponents: Evaluate any exponential expressions next (none in this practice test).
• Multiplication and Division: Evaluate multiplication and division operations from left to right.
• Addition and Subtraction: Finally, evaluate any addition and subtraction operations from left to right.

Why is the Order of Operations Important?

The order of operations is essential in mathematics because it provides a standard procedure for evaluating expressions, ensuring that calculations are performed accurately and consistently. Without a standardized order of operations, mathematical expressions can be ambiguous, leading to errors and confusion.

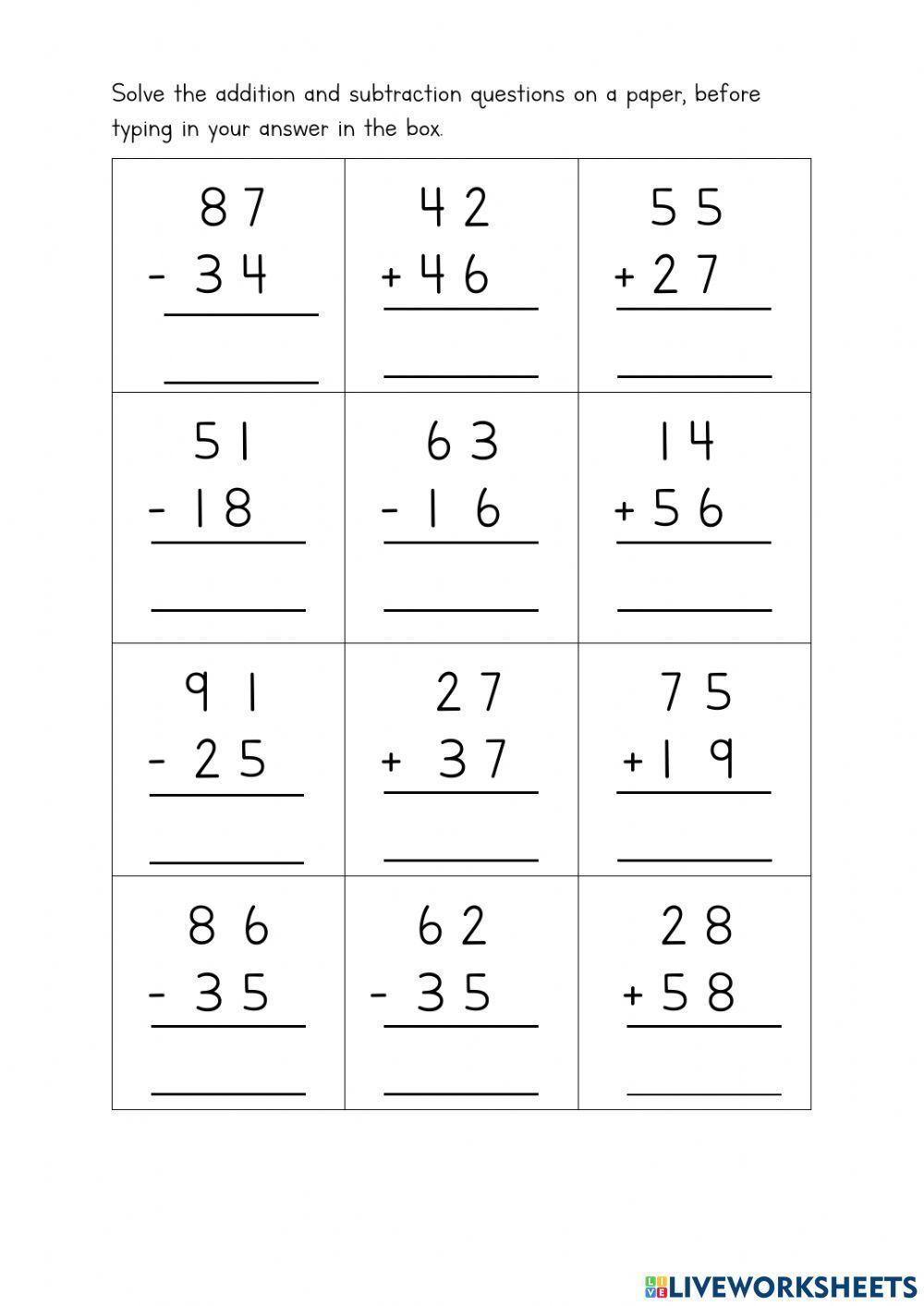
Practice Test 1: Simple Expressions

Try your hand at these simple expressions to get a feel for the order of operations:

1. 2 + 3 × 4 =
2. 12 - 8 + 2 =
3. 9 - 3 + 1 =
4. 7 × 2 - 1 =
5. 15 + 2 - 8 =

Check your answers against the solutions below:

Solutions to Practice Test 1

1. 2 + 3 × 4 = 2 + 12 = 14
2. 12 - 8 + 2 = 4 + 2 = 6
3. 9 - 3 + 1 = 6 + 1 = 7
4. 7 × 2 - 1 = 14 - 1 = 13
5. 15 + 2 - 8 = 17 - 8 = 9

Practice Test 2: Expressions with Parentheses

Now, let’s introduce parentheses to the mix:

1. (2 + 3) × 4 =
2. 12 - (8 - 2) =
3. (9 - 3) + 1 =
4. 7 × (2 - 1) =
5. (15 + 2) - 8 =

Check your answers against the solutions below:

Solutions to Practice Test 2

1. (2 + 3) × 4 = 5 × 4 = 20
2. 12 - (8 - 2) = 12 - 6 = 6
3. (9 - 3) + 1 = 6 + 1 = 7
4. 7 × (2 - 1) = 7 × 1 = 7
5. (15 + 2) - 8 = 17 - 8 = 9

Practice Test 3: Multi-Step Expressions

Try these more challenging expressions that require multiple steps:

1. 18 - 3 × 2 + 4 =
2. 24 ÷ 4 + 2 - 1 =
3. 9 × 2 - 15 + 3 =
4. 48 ÷ 6 - 2 + 5 =
5. 11 × 3 - 4 - 2 =

Check your answers against the solutions below:

Solutions to Practice Test 3

1. 18 - 3 × 2 + 4 = 18 - 6 + 4 = 16
2. 24 ÷ 4 + 2 - 1 = 6 + 2 - 1 = 7
3. 9 × 2 - 15 + 3 = 18 - 15 + 3 = 6
4. 48 ÷ 6 - 2 + 5 = 8 - 2 + 5 = 11
5. 11 × 3 - 4 - 2 = 33 - 4 - 2 = 27

🤔 Note: Remember to follow the order of operations when evaluating expressions.Parentheses first, then multiplication and division, and finally addition and subtraction.

Practice makes perfect! Keep honing your skills with more practice tests and exercises. You got this!

By mastering the order of operations, you’ll become more confident and proficient in your mathematical abilities. Keep practicing, and soon you’ll be tackling even the most complex expressions with ease!

Related Terms:

• Order of Operations Worksheet PDF
• Order of operations with exponents
• Order of Operations Scaffolded Worksheet