Fraction Operations: Add, Subtract, Multiply, Divide Worksheets
Understanding Fraction Operations: A Comprehensive Guide
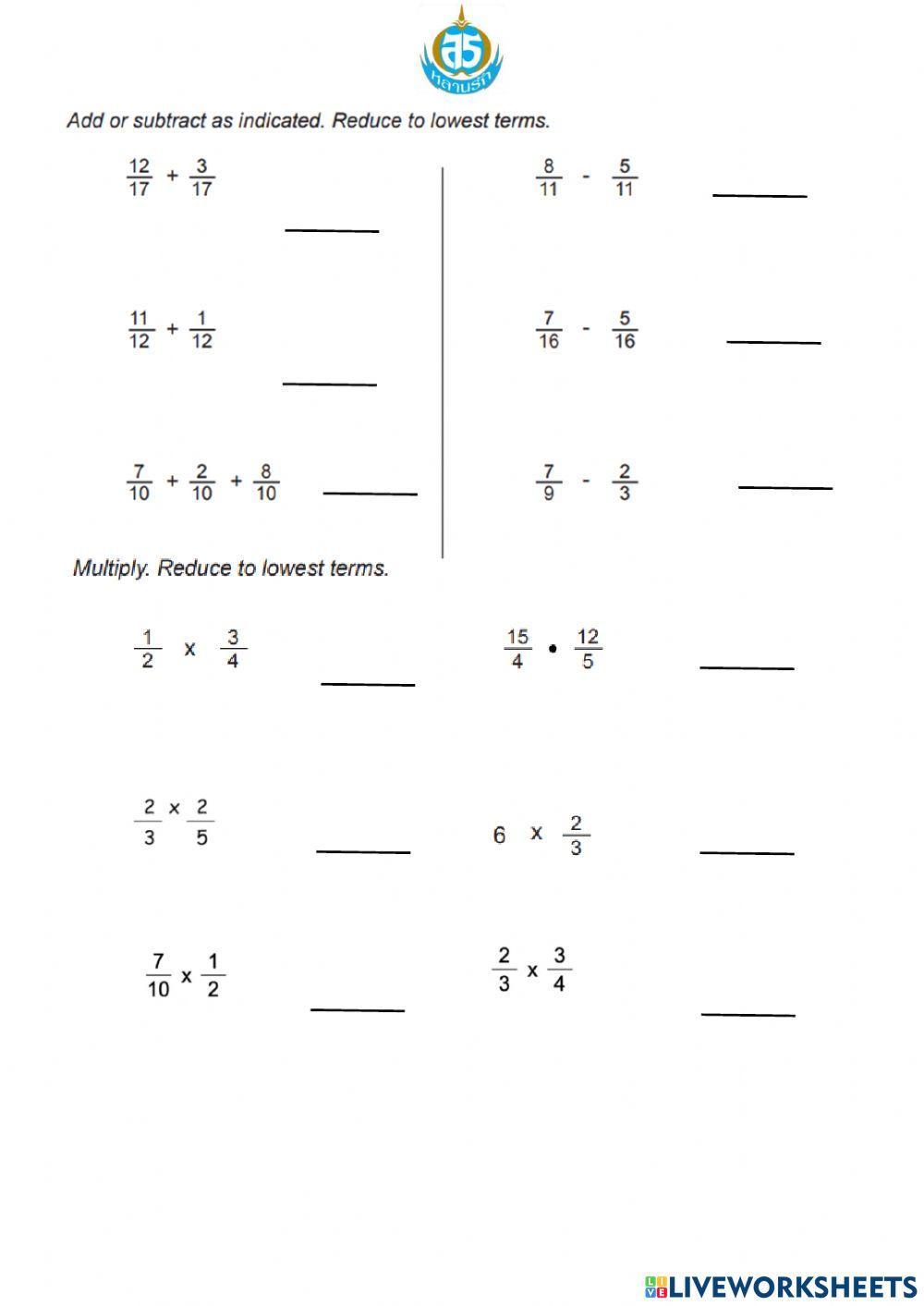
Fraction operations are a fundamental concept in mathematics, and mastering them is crucial for success in various mathematical disciplines. In this article, we will delve into the world of fraction operations, exploring the four primary operations: addition, subtraction, multiplication, and division. We will provide step-by-step instructions, examples, and worksheets to help you solidify your understanding of these essential math concepts.
Addition of Fractions
Adding fractions is a straightforward process that requires a few simple steps. To add fractions, you need to follow these rules:
- Step 1: Ensure the fractions have the same denominator. If not, find the least common multiple (LCM) of the denominators and convert the fractions to have the LCM as the denominator.
- Step 2: Add the numerators while keeping the denominator the same.
- Step 3: Simplify the resulting fraction, if possible.

| Example | Step-by-Step Solution | Result |
|---|---|---|
| 1/4 + 1/4 | Since the denominators are the same (4), add the numerators: 1 + 1 = 2. Keep the denominator the same (4). | 2/4 = 1/2 |
| 1/6 + 1/8 | Find the LCM of 6 and 8, which is 24. Convert both fractions: 4/24 + 3/24. Add the numerators: 4 + 3 = 7. Keep the denominator the same (24). | 7/24 |
Subtraction of Fractions
Subtracting fractions follows a similar process to adding fractions, with a slight modification:
- Step 1: Ensure the fractions have the same denominator. If not, find the LCM of the denominators and convert the fractions to have the LCM as the denominator.
- Step 2: Subtract the numerators while keeping the denominator the same.
- Step 3: Simplify the resulting fraction, if possible.
| Example | Step-by-Step Solution | Result |
|---|---|---|
| 3/4 - 1/4 | Since the denominators are the same (4), subtract the numerators: 3 - 1 = 2. Keep the denominator the same (4). | 2/4 = 1/2 |
| 5/8 - 3/8 | Since the denominators are the same (8), subtract the numerators: 5 - 3 = 2. Keep the denominator the same (8). | 2/8 = 1/4 |
Multiplication of Fractions
Multiplying fractions is a relatively simple process:
- Step 1: Multiply the numerators.
- Step 2: Multiply the denominators.
- Step 3: Simplify the resulting fraction, if possible.
| Example | Step-by-Step Solution | Result |
|---|---|---|
| 1/2 × 3/4 | Multiply the numerators: 1 × 3 = 3. Multiply the denominators: 2 × 4 = 8. | 3/8 |
| 2/3 × 3/5 | Multiply the numerators: 2 × 3 = 6. Multiply the denominators: 3 × 5 = 15. | 6/15 = 2/5 |
Division of Fractions
Dividing fractions requires a slight modification to the multiplication process:
- Step 1: Invert the second fraction (i.e., flip the numerator and denominator).
- Step 2: Multiply the fractions as usual.
- Step 3: Simplify the resulting fraction, if possible.
| Example | Step-by-Step Solution | Result |
|---|---|---|
| 1/2 ÷ 3/4 | Invert the second fraction: 3/4 becomes 4/3. Multiply the fractions: 1/2 × 4/3. | 4/6 = 2/3 |
| 2/3 ÷ 3/5 | Invert the second fraction: 3/5 becomes 5/3. Multiply the fractions: 2/3 × 5/3. | 10/9 |
🤔 Note: When dividing fractions, it's essential to invert the second fraction to ensure accurate results.
Worksheets and Practice
To reinforce your understanding of fraction operations, try practicing with these worksheets:
- Addition of Fractions: Practice adding fractions with the same denominator and different denominators.
- Subtraction of Fractions: Practice subtracting fractions with the same denominator and different denominators.
- Multiplication of Fractions: Practice multiplying fractions with different numerators and denominators.
- Division of Fractions: Practice dividing fractions with different numerators and denominators.
What is the least common multiple (LCM) of two numbers?
+The least common multiple (LCM) of two numbers is the smallest number that is a multiple of both numbers.
How do I simplify a fraction?
+To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator, and divide both numbers by the GCD.
Can I add or subtract fractions with different denominators?
+No, you cannot add or subtract fractions with different denominators directly. You need to find the least common multiple (LCM) of the denominators and convert the fractions to have the LCM as the denominator.
How do I divide fractions?
+To divide fractions, invert the second fraction (i.e., flip the numerator and denominator) and multiply the fractions as usual.
Mastering fraction operations is essential for success in mathematics. By understanding how to add, subtract, multiply, and divide fractions, you’ll be able to tackle more complex mathematical concepts with confidence. Remember to practice regularly and use the worksheets provided to reinforce your understanding of fraction operations.