Multi Step Equations Worksheets
Unlocking the Power of Multi-Step Equations: A Comprehensive Guide
Mathematics is a subject that requires patience, practice, and dedication. As students progress in their mathematical journey, they encounter various types of equations that challenge their problem-solving skills. One such type of equation is the multi-step equation, which requires students to apply multiple mathematical operations to solve for the unknown variable. In this article, we will delve into the world of multi-step equations, exploring their significance, types, and providing worksheets for practice.
What are Multi-Step Equations?
A multi-step equation is an equation that requires more than one mathematical operation to solve for the unknown variable. These equations can involve addition, subtraction, multiplication, division, or a combination of these operations. The key characteristic of multi-step equations is that they cannot be solved in a single step, requiring students to break down the equation into manageable parts and apply the correct mathematical operations to arrive at the solution.
Types of Multi-Step Equations
There are several types of multi-step equations, including:
- Linear Equations: These equations involve a single variable and can be solved using addition, subtraction, multiplication, or division.
- Quadratic Equations: These equations involve a squared variable and can be solved using factoring, quadratic formula, or other algebraic methods.
- Rational Equations: These equations involve fractions and can be solved using algebraic methods, such as cross-multiplication.
How to Solve Multi-Step Equations
Solving multi-step equations requires a systematic approach. Here are the general steps to follow:
- Read the equation carefully: Identify the variable and the mathematical operations involved.
- Break down the equation: Separate the equation into manageable parts, identifying the operations required to solve for the variable.
- Apply the correct mathematical operations: Use the order of operations (PEMDAS) to ensure that the correct operations are applied in the correct order.
- Simplify the equation: Combine like terms and simplify the equation to arrive at the solution.
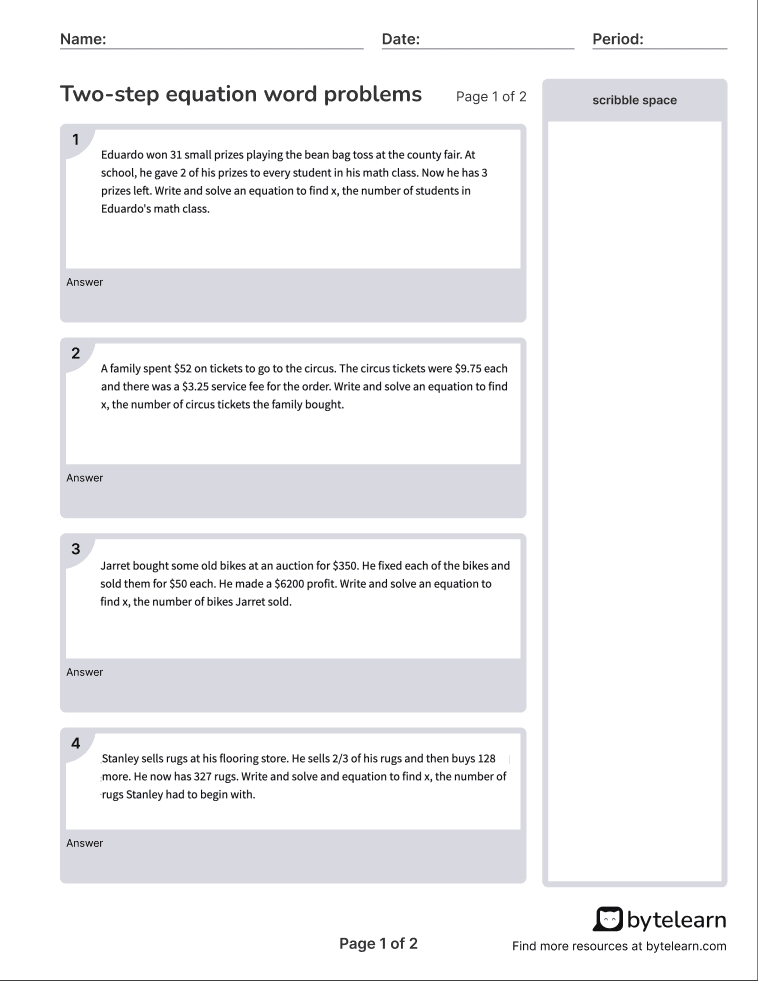
Multi-Step Equations Worksheets
Practice is essential to mastering multi-step equations. Here are some worksheets to help students practice:
Worksheet 1: Linear Equations

| Equation | Solution |
|---|---|
| 2x + 5 = 11 | x = 3 |
| x - 3 = 7 | x = 10 |
| 4x = 28 | x = 7 |
Worksheet 2: Quadratic Equations
| Equation | Solution |
|---|---|
| x^2 + 4x + 4 = 0 | x = -2 |
| x^2 - 7x + 12 = 0 | x = 3, 4 |
| x^2 + 2x - 6 = 0 | x = -3, 2 |
Worksheet 3: Rational Equations
| Equation | Solution |
|---|---|
| 1/x + 2 = 3 | x = 1/3 |
| 2/x - 1 = 1/2 | x = 4/3 |
| x/2 + 1 = 3/4 | x = 1/2 |
📝 Note: These worksheets are meant to provide practice and are not exhaustive. Students should attempt to solve the equations on their own before referring to the solutions.
As students practice solving multi-step equations, they develop problem-solving skills, critical thinking, and analytical reasoning. These skills are essential in mathematics and other subjects, enabling students to tackle complex problems with confidence.
In conclusion, multi-step equations are an integral part of mathematics, requiring students to apply mathematical operations to solve for the unknown variable. By understanding the types of multi-step equations, following the steps to solve them, and practicing with worksheets, students can master this concept and develop essential problem-solving skills.
What is the difference between a linear equation and a quadratic equation?
+A linear equation involves a single variable and can be solved using addition, subtraction, multiplication, or division. A quadratic equation involves a squared variable and can be solved using factoring, quadratic formula, or other algebraic methods.
How do I solve a rational equation?
+To solve a rational equation, cross-multiply the fractions, simplify the equation, and solve for the variable using algebraic methods.
What is the order of operations (PEMDAS)?
+PEMDAS stands for Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction. It is the order in which mathematical operations should be performed when solving an equation.