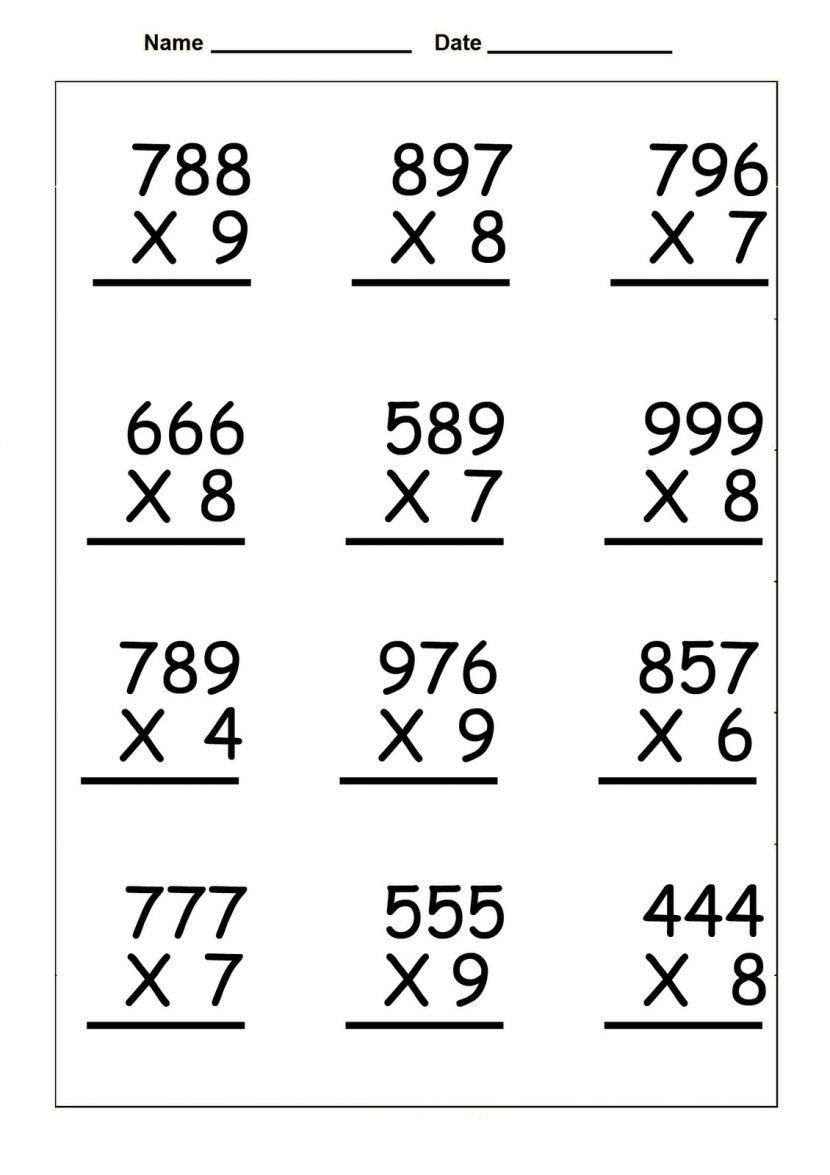
Midpoint Formula Worksheet: Find Midpoints with Ease

Understanding the Midpoint Formula
The midpoint formula is a fundamental concept in coordinate geometry, enabling you to find the middle point of a line segment given the coordinates of its endpoints. This formula is widely used in various mathematical and real-world applications, such as graphing, geometry, and physics.
What is the Midpoint Formula?
The midpoint formula states that the coordinates of the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) are given by:
(xm, ym) = ((x1 + x2) / 2, (y1 + y2) / 2)
where (xm, ym) represents the coordinates of the midpoint.
How to Use the Midpoint Formula
Using the midpoint formula is straightforward. Here’s a step-by-step guide:
- Identify the coordinates of the endpoints of the line segment. Let’s call these points (x1, y1) and (x2, y2).
- Add the x-coordinates of the endpoints: x1 + x2.
- Divide the sum of the x-coordinates by 2: (x1 + x2) / 2.
- Add the y-coordinates of the endpoints: y1 + y2.
- Divide the sum of the y-coordinates by 2: (y1 + y2) / 2.
- The resulting coordinates ((x1 + x2) / 2, (y1 + y2) / 2) represent the midpoint of the line segment.
📝 Note: Make sure to follow the order of operations (PEMDAS) when evaluating the expressions.
Examples and Practice Problems
Here are some examples to help you practice using the midpoint formula:
- Find the midpoint of the line segment with endpoints (3, 4) and (5, 6).
- Find the midpoint of the line segment with endpoints (-2, 3) and (4, -5).
- Find the midpoint of the line segment with endpoints (1, 1) and (3, 3).
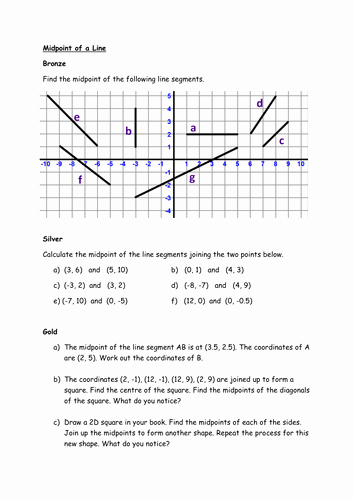
| Endpoints | Midpoint |
|---|---|
| (3, 4) and (5, 6) | ((3 + 5) / 2, (4 + 6) / 2) = (4, 5) |
| (-2, 3) and (4, -5) | ((-2 + 4) / 2, (3 + (-5)) / 2) = (1, -1) |
| (1, 1) and (3, 3) | ((1 + 3) / 2, (1 + 3) / 2) = (2, 2) |
Common Mistakes to Avoid
When using the midpoint formula, be sure to avoid the following common mistakes:
- Reversing the order of operations: Make sure to follow the order of operations (PEMDAS) when evaluating the expressions.
- Forgetting to divide by 2: Remember to divide the sum of the coordinates by 2 to find the midpoint.
- Using the wrong coordinates: Double-check that you are using the correct coordinates for the endpoints.
Real-World Applications
The midpoint formula has numerous real-world applications, such as:
- Graphing: Finding the midpoint of a line segment can help you graph a function or a shape more accurately.
- Geometry: The midpoint formula is used in various geometric calculations, such as finding the center of a circle or the midpoint of an arc.
- Physics: The midpoint formula can be used to find the midpoint of a trajectory or the center of mass of an object.
Summarizing the key points, the midpoint formula is a fundamental concept in coordinate geometry that enables you to find the middle point of a line segment given the coordinates of its endpoints. By following the step-by-step guide and practicing with examples, you can master the midpoint formula and apply it to various real-world applications.
What is the midpoint formula?
+The midpoint formula is a mathematical formula that calculates the midpoint of a line segment given the coordinates of its endpoints. The formula is (xm, ym) = ((x1 + x2) / 2, (y1 + y2) / 2).
How do I use the midpoint formula?
+To use the midpoint formula, identify the coordinates of the endpoints, add the x-coordinates and divide by 2, and add the y-coordinates and divide by 2.
What are some common mistakes to avoid when using the midpoint formula?
+Common mistakes to avoid include reversing the order of operations, forgetting to divide by 2, and using the wrong coordinates.