Linear vs Nonlinear Functions Worksheet Guide
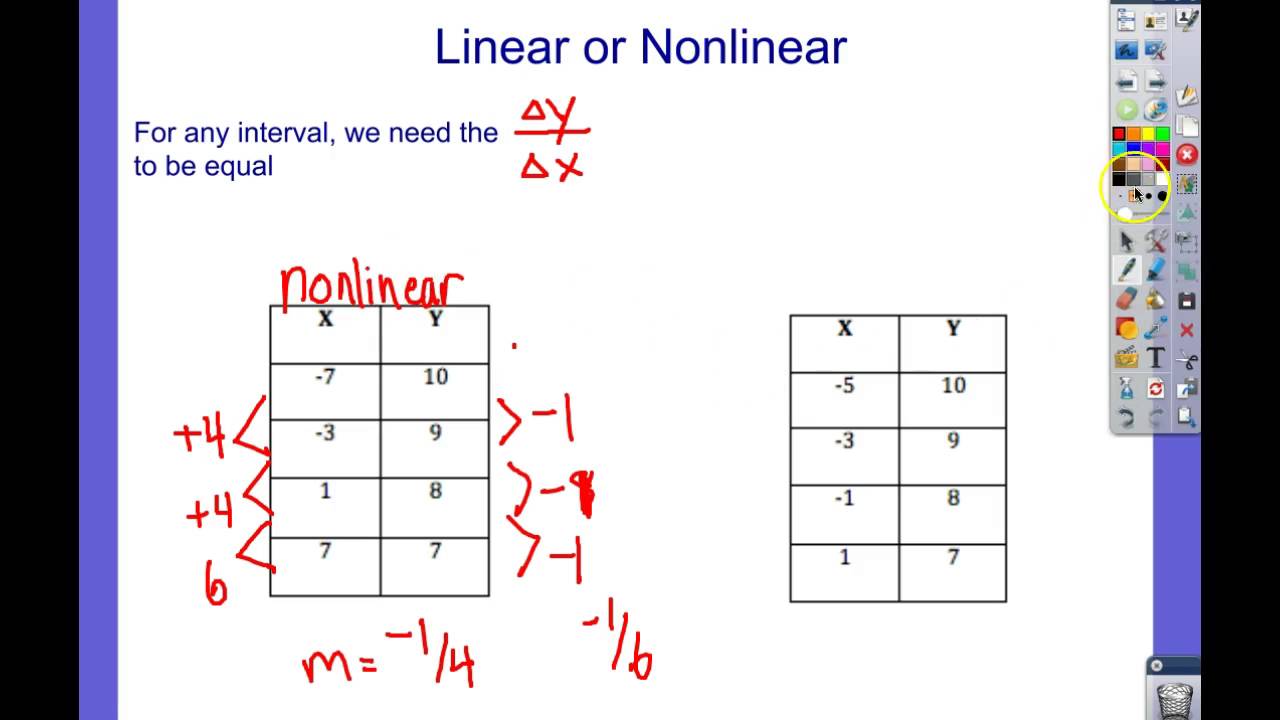
Linear vs Nonlinear Functions Worksheet Guide
Linear and nonlinear functions are two fundamental concepts in mathematics, particularly in algebra. Understanding the differences between these two types of functions is crucial for solving equations, graphing, and modeling real-world problems. In this guide, we will explore the definitions, characteristics, and examples of linear and nonlinear functions, providing a comprehensive worksheet guide for students and teachers.
What are Linear Functions?
Linear functions are polynomial functions of degree one, which means the highest power of the variable (usually x) is one. They are characterized by a constant rate of change, resulting in a straight line when graphed. The general form of a linear function is:
f(x) = mx + b
where:
- f(x) is the function
- x is the input or independent variable
- m is the slope or rate of change
- b is the y-intercept or constant term
Examples of linear functions include:
- f(x) = 2x + 3
- f(x) = x - 2
- f(x) = 4x - 5
Characteristics of Linear Functions
Linear functions have several key characteristics:
- Constant Rate of Change: The rate of change of a linear function is constant, meaning that the output changes by the same amount for each unit change in the input.
- Straight Line Graph: Linear functions graph as straight lines, making it easy to visualize and analyze.
- Proportionality: Linear functions exhibit proportionality, meaning that the output is directly proportional to the input.
What are Nonlinear Functions?
Nonlinear functions, on the other hand, are functions that are not linear. They can have varying rates of change, resulting in curved or irregular graphs. Nonlinear functions can be polynomial functions of degree two or higher, rational functions, exponential functions, or trigonometric functions.
Examples of nonlinear functions include:
- f(x) = x^2 + 3x - 4
- f(x) = 1 / (x + 1)
- f(x) = 2^x
- f(x) = sin(x)
Characteristics of Nonlinear Functions
Nonlinear functions have several key characteristics:
- Varying Rate of Change: Nonlinear functions have a varying rate of change, meaning that the output changes by different amounts for each unit change in the input.
- Curved or Irregular Graph: Nonlinear functions graph as curves or irregular shapes, making them more challenging to visualize and analyze.
- Non-Proportionality: Nonlinear functions do not exhibit proportionality, meaning that the output is not directly proportional to the input.
Comparing Linear and Nonlinear Functions
Here’s a summary of the key differences between linear and nonlinear functions:
| Characteristic | Linear Functions | Nonlinear Functions |
|---|---|---|
| Rate of Change | Constant | Varying |
| Graph | Straight Line | Curved or Irregular |
| Proportionality | Proportional | Non-Proportional |
| Degree | Degree 1 | Degree 2 or Higher |
📝 Note: This table highlights the main differences between linear and nonlinear functions, but it's essential to remember that there are many variations and exceptions within each category.
Worksheet Guide
To help students and teachers practice identifying and working with linear and nonlinear functions, here are some worksheet guide questions:
- Identify whether the following functions are linear or nonlinear:
- f(x) = 2x + 1
- f(x) = x^2 - 3x + 2
- f(x) = 1 / (x - 2)
- Graph the following linear functions:
- f(x) = x - 2
- f(x) = 2x + 1
- f(x) = x + 3
- Determine the slope and y-intercept of the following linear functions:
- f(x) = 2x - 3
- f(x) = x + 2
- f(x) = 3x - 4
- Identify the characteristics of the following nonlinear functions:
- f(x) = x^2 + 2x - 3
- f(x) = 1 / (x + 1)
- f(x) = 2^x
- Create a table to compare the characteristics of linear and nonlinear functions.
What is the main difference between linear and nonlinear functions?
+The main difference between linear and nonlinear functions is the rate of change. Linear functions have a constant rate of change, resulting in a straight line graph, while nonlinear functions have a varying rate of change, resulting in curved or irregular graphs.
How can I identify whether a function is linear or nonlinear?
+To identify whether a function is linear or nonlinear, look at the equation and graph. Linear functions have a constant slope and a straight line graph, while nonlinear functions have a varying slope and a curved or irregular graph.
What are some real-world examples of linear and nonlinear functions?
+Linear functions can be used to model real-world situations such as cost-benefit analysis, while nonlinear functions can be used to model population growth, financial transactions, and electrical circuits.
In conclusion, understanding the differences between linear and nonlinear functions is essential for solving equations, graphing, and modeling real-world problems. By recognizing the characteristics of each type of function, students and teachers can better analyze and work with functions in various mathematical contexts.