Mastering Fractions: A Beginner's Worksheet Guide
Understanding Fractions: The Basics
Fractions are a fundamental concept in mathematics, representing a part of a whole. They consist of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
For example, in the fraction 3⁄4, the numerator is 3 and the denominator is 4. This means we have 3 equal parts out of a total of 4 parts.
Types of Fractions
There are several types of fractions, including:
- Proper Fractions: These are fractions where the numerator is less than the denominator. Example: 3⁄4
- Improper Fractions: These are fractions where the numerator is greater than or equal to the denominator. Example: 5⁄3
- Mixed Numbers: These are fractions that consist of a whole number and a proper fraction. Example: 2 3⁄4
Adding and Subtracting Fractions
To add or subtract fractions, we need to follow these steps:
- Find a Common Denominator: We need to find a common denominator for both fractions. This can be done by finding the least common multiple (LCM) of the two denominators.
- Convert to Equivalent Fractions: We convert both fractions to equivalent fractions with the common denominator.
- Add or Subtract: We add or subtract the numerators, keeping the denominator the same.
Example: Add 1⁄4 and 1⁄6
- Find a common denominator: LCM of 4 and 6 is 12
- Convert to equivalent fractions: 1⁄4 = 3⁄12 and 1⁄6 = 2⁄12
- Add: 3⁄12 + 2⁄12 = 5⁄12
Multiplying Fractions
To multiply fractions, we simply multiply the numerators and multiply the denominators.
Example: Multiply 2⁄3 and 3⁄4
- Multiply numerators: 2 x 3 = 6
- Multiply denominators: 3 x 4 = 12
- Result: 6⁄12 = 1⁄2
Dividing Fractions
To divide fractions, we invert the second fraction (i.e., flip the numerator and denominator) and then multiply.
Example: Divide 2⁄3 by 3⁄4
- Invert the second fraction: 3⁄4 becomes 4⁄3
- Multiply: 2⁄3 x 4⁄3 = 8⁄9
Fraction Worksheet
Here is a worksheet to help you practice working with fractions:
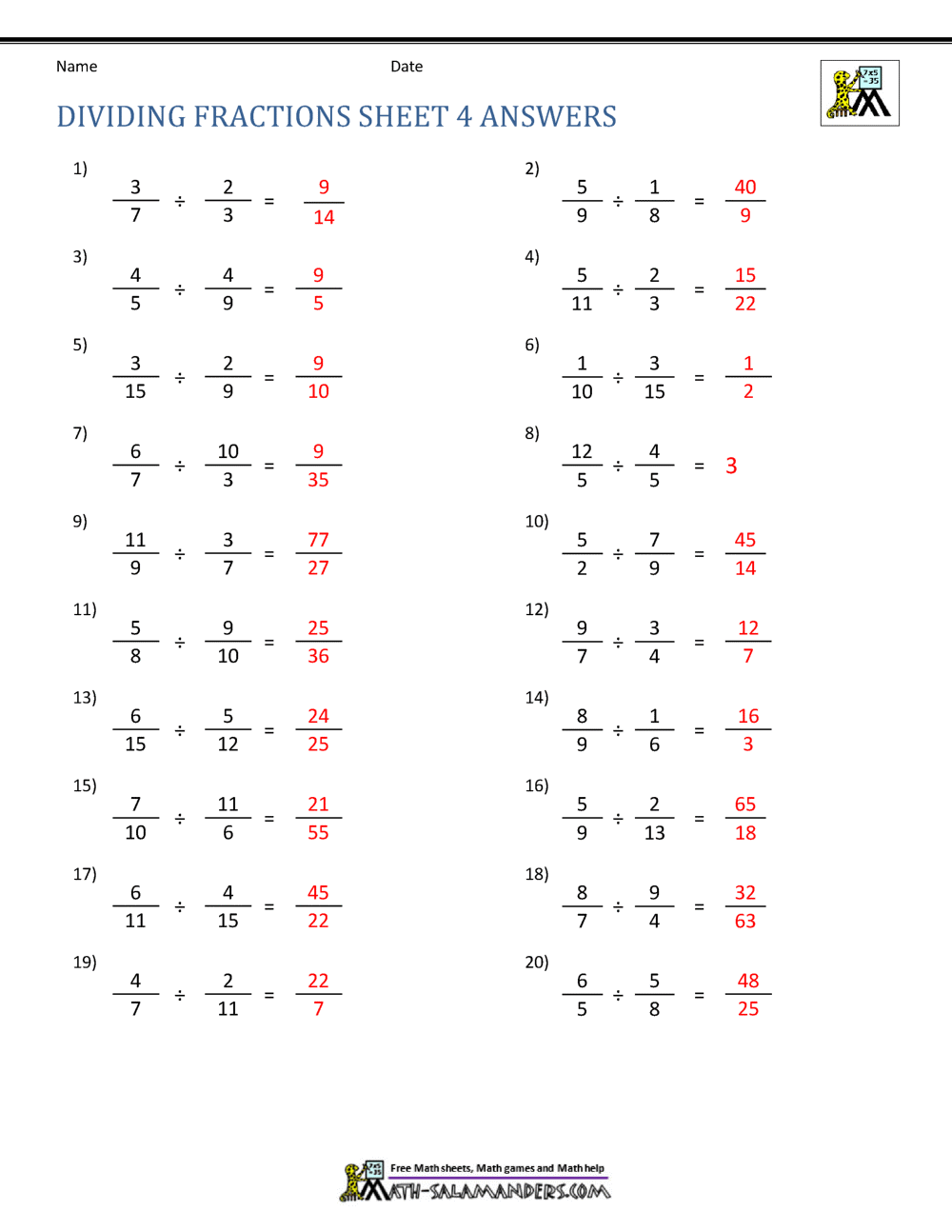
| Fraction 1 | Fraction 2 | Operation | Result |
|---|---|---|---|
| 1/2 | 1/4 | Add | _____ |
| 3/4 | 2/3 | Multiply | _____ |
| 2/3 | 3/4 | Divide | _____ |
| 1/4 | 1/6 | Subtract | _____ |
📝 Note: Remember to find a common denominator when adding or subtracting fractions, and to invert the second fraction when dividing fractions.
Simplifying Fractions
Simplifying fractions means finding the simplest form of a fraction. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and denominator.
Example: Simplify 6⁄8
- Find the GCD: GCD of 6 and 8 is 2
- Divide both numerator and denominator by the GCD: 6 ÷ 2 = 3 and 8 ÷ 2 = 4
- Result: 3⁄4
Conclusion
Mastering fractions takes practice and patience. By following the steps outlined in this guide and practicing with the worksheet, you’ll become more confident in your ability to work with fractions. Remember to always find a common denominator when adding or subtracting fractions, and to invert the second fraction when dividing fractions.
What is a fraction?
+A fraction is a way of expressing a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number).
How do I add fractions?
+To add fractions, you need to find a common denominator, convert both fractions to equivalent fractions with the common denominator, and then add the numerators.
How do I simplify a fraction?
+To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and denominator, and then divide both numbers by the GCD.
Related Terms:
- Introduction to Fractions Worksheet PDF
- Fraction Worksheet Grade 5
- Fractions worksheets with answers PDF
- Fractions worksheets PDF Grade 7
- Basic Fractions Worksheet with answers
- Fraction Worksheet Grade 4